目录
上一篇总结了下线性结构 - 算法-数据结构基础1,这一篇文章来讲下非线性结构
非线性结构
树
树(Tree)是n(n>=0)个节点的有限集合。当n=0时是空树,任何非空树的特点为:
- 有且只有一个根节点(Root)
- 当n>1时,其节点可分为m(m>0)个互不相交的有限集,每一个集合本身又是一个树,并称为树的子树。
- 除根节点外,每个节点有且仅有一个父节点,没有子节点的节点称为叶子节点(Leaf)
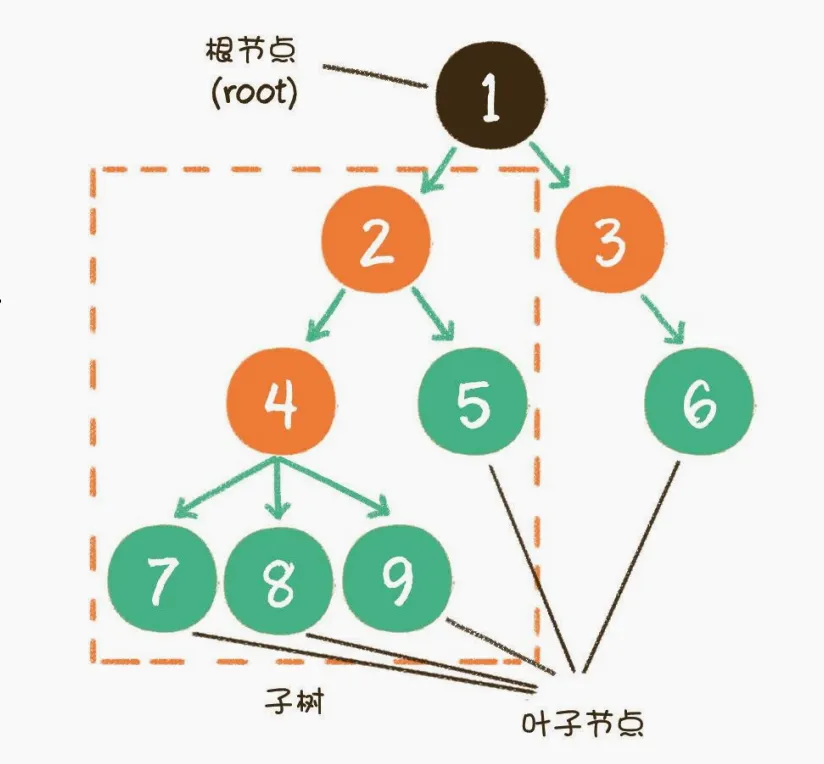
核心术语
| 术语 | 说明 | 图示示例 |
|---|---|---|
| 度 | 节点的子节点数量 | 根节点度为3 |
| 层次 | 根为第1层,子节点层次=父节点+1 | 叶子节点在第4层 |
| 高度 | 树中节点的最大层次 | 图示树高度为4 |
| 子树 | 由某节点及其后代构成的树结构 | 节点1的子树 |
二叉树
二叉树(binary tree)是树的一种特殊形式。二叉,顾名思义,这种树的每个节点最多有2个孩子节点。注意,这里是最多有2个,也可能只有1个,或者没有孩子节点。这两个孩子节点的顺序是固定的,就像人的左手就是左手,右手就是右手,不能够颠倒或混淆。
- 左子节点(Left Child)
- 右子节点(Right Child)
二叉树还有两种特殊结构,一个叫作满二又树,另一个叫作完全二叉树。
什么是满二叉树呢?
一个二又树的所有非叶子节点都存在左孩子和右孩子,并且所有叶子节点都在同一层级上,那么这个树就是满二叉树。简单点说,满二叉树的每一个分支都是满的。
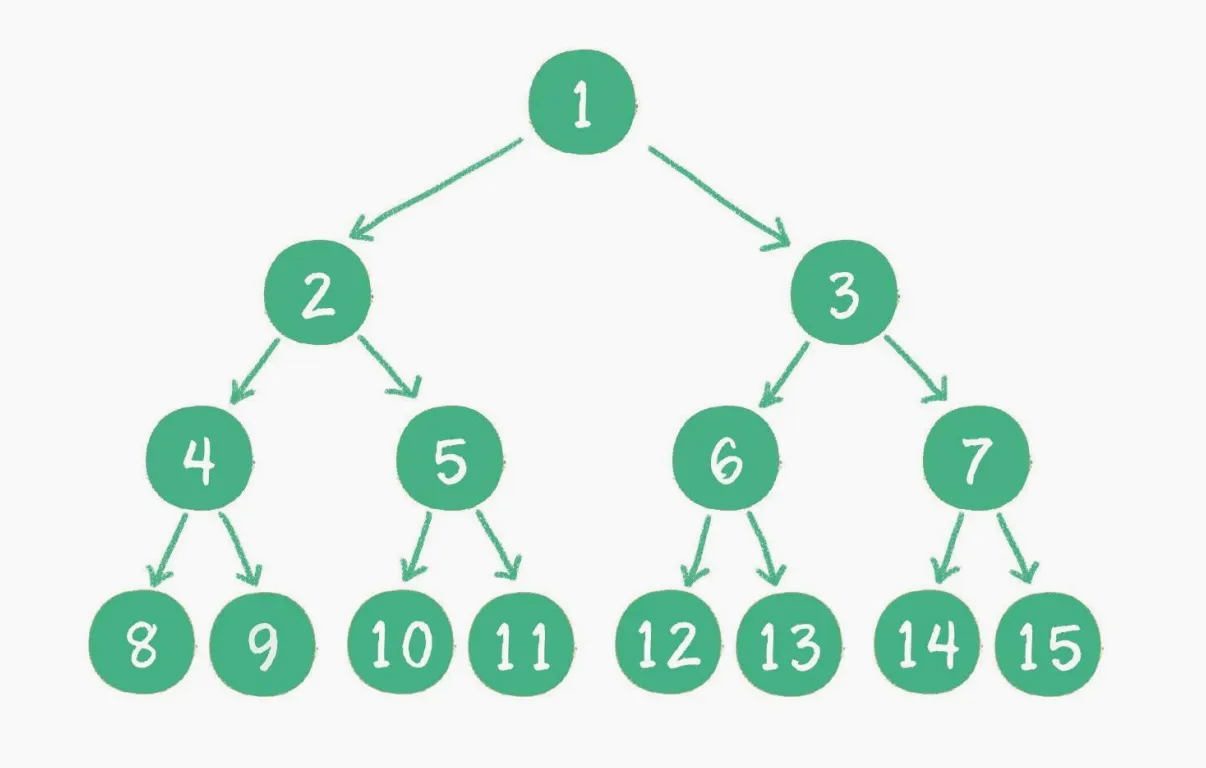
什么是完全二叉树呢?
对一个有n个节点的二叉树,按层级顺序编号,则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同,则这个二又树为完全二叉树。
这个定义还真绕,看看下图就很容易理解了。
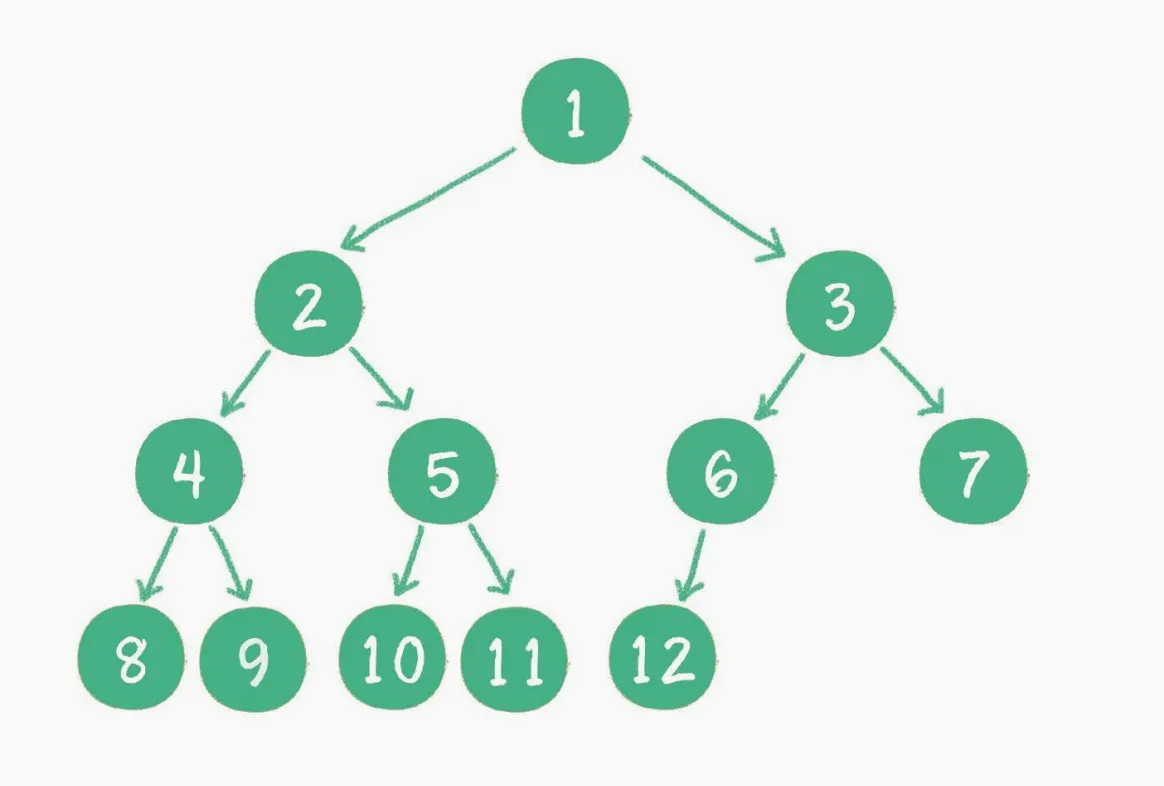
在上图中,二又树编号从1到12的12个节点,和前面满二叉树编号从1到12的节点位置完全对应。因此这个树是完全二叉树。
提示
完全二叉树之最后一个节点之前的节点都存在,则是完全二叉树,一个子树中必须先有左节点,再有右节点,如果上述图中的没有左节点12,而是存在右节点的13,那此树则不是完全二叉树
二叉树的遍历
二叉树是典型的非线性数据结构,遍历时需要把非线性关联的节点转化成一个线性的序列。以不同的方式来遍历,遍历出的序列顺序也不同。从宏观的角度来说,二又树的遍历归结为两大类。
- 深度优先遍历(DFS)
- 广度优先遍历(BFS)
相关信息
深度优先和广度优先这两个概念不止局限于二叉树,它们更是一种抽象的算法思想,决定了访问某些复杂数据结构的顺序。
深度优先遍历(DFS)
所谓深度优先,顾名思义,就是偏向于纵深,“一头扎到底”的访问方式。可以分为3种遍历方式
- 前序遍历。
- 中序遍历。
- 后序遍历。
理解遍历的顺序
以上3种遍历方式,分前中后,实际指的是根节点(Root)的位置,根节点在前,那就是前序遍历,根节点在中间,那就是中序遍历,根节点在最后,那就是后续遍历,其中无论什么遍历,同一个子树下的左子节点一定比右子节点先遍历
前序遍历
二叉树的前序遍历,输出顺序是根节点、左子树、右子树。
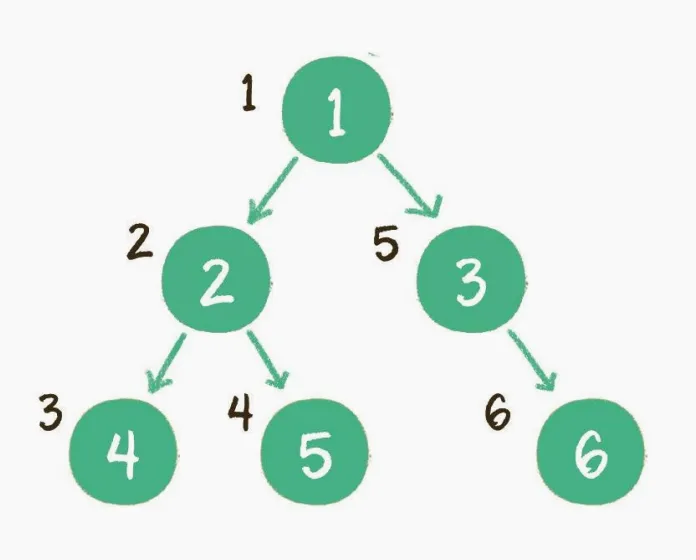
- 首先输出的是根节点1。
- 由于根节点1存在左孩子,输出左孩子节点2.
- 由于节点2也存在左孩子,输出左孩子节点4。
- 节点4既没有左孩子,也没有右孩子,那么回到节点2,输出节点2的右孩子节点5。
- 节点5既没有左孩子,也没有右孩子,那么回到节点1,输出节点1的右孩子节点3。
- 节点3没有左孩子,但是有右孩子,因此输出节点3的右孩子节点6。
中序遍历
二叉树的中序遍历,输出顺序是左子树、根节点、右子树。
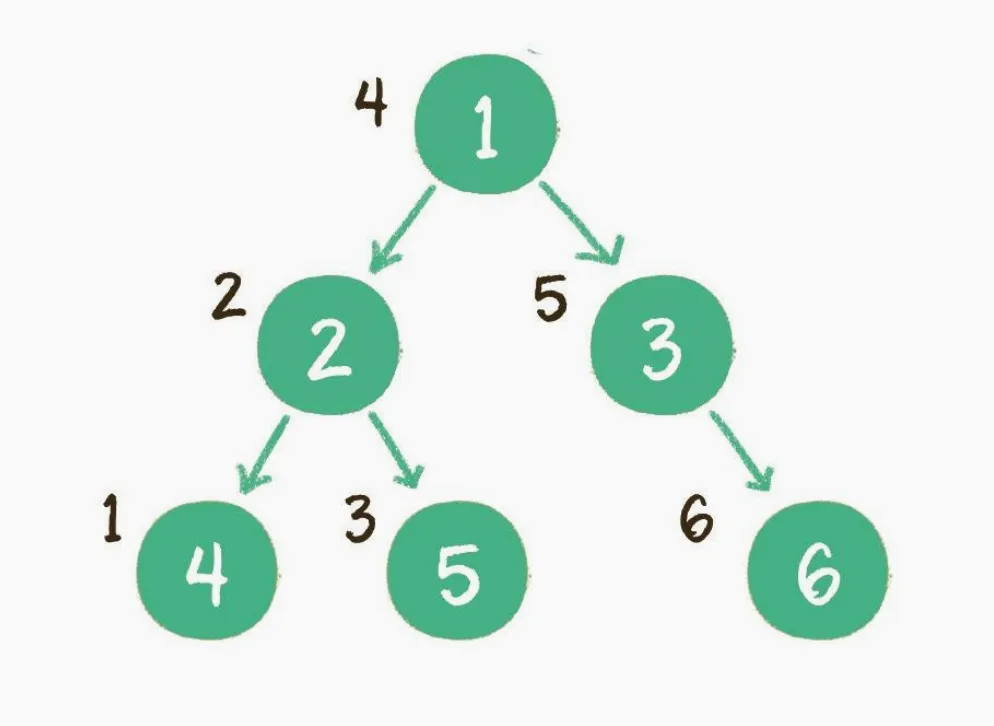
- 首先访问根节点的左孩子,如果这个左孩子还拥有左孩子,则继续深入访问下去,一直找到不再有左孩子的节点,并输出该节点。显然,第一个没有左孩子的节点是节点4。
- 依照中序遍历的次序,接下来输出节点4的父节点2。
- 再输出节点2的右孩子节点5.
- 以节点2为根的左子树已经输出完毕,这时再输出整个二叉树的根节点1。
- 由于节点3没有左孩子,所以直接输出根节点1的右孩子节点3。
- 最后输出节点3的右孩子节点6。
后序遍历
二叉树的后序遍历,输出顺序是左子树、右子树、根节点。
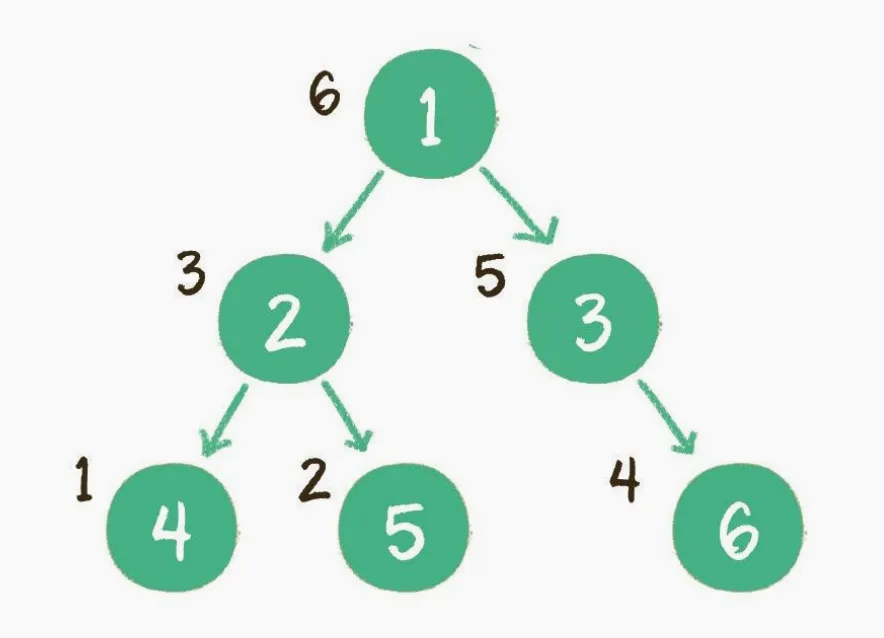
上图就是一个二又树的后序遍历,每个节点左侧的序号代表该节点的输出顺序。 由于二叉树的后序遍历和前序、中序遍历的思想大致相同,这里就不再列举细节了。
代码实现
二叉树用递归方式来实现前序、中序、后序遍历,是最为自然的方式,因此代码也非常简单。
javapublic class Test {
// 二叉树节点定义
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int val) {
this.val = val;
}
}
static class Traversal {
// 递归前序遍历
void preOrder(TreeNode root) {
if (root == null) return;
System.out.print(root.val + " "); // 访问根
preOrder(root.left);
preOrder(root.right);
}
// 中序遍历
void inOrder(TreeNode root) {
if(root == null) return;
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}
// 递归后序遍历
void postOrder(TreeNode root) {
if (root == null) return;
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val + " ");
}
}
public static void main(String[] args) {
// 构建二叉树
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.right = new TreeNode(6);
// 前序遍历
System.out.print("前序遍历:");
new Traversal().preOrder(root);
System.out.println();
// 中序遍历
System.out.print("中序遍历:");
new Traversal().inOrder(root);
System.out.println();
// 后序遍历
System.out.print("后序遍历:");
new Traversal().postOrder(root);
}
}
// 输出结果
前序遍历:1 2 4 5 3 6
中序遍历:4 2 5 1 3 6
后序遍历:4 5 2 6 3 1
这3种遍历方式的区别,仅仅是输出的执行位置不同:前序遍历的输出在前,中遍历的输出在中间,后序遍历的输出在最后。
代码中值得注意的一点是二叉树的构建。二叉树的构建方法有很多,这里把一个线性的链表转化成非线性的二叉树,链表节点的顺序恰恰是二叉树前序遍历的顺序。链表中的空值,代表二又树节点的左孩子或右孩子为空的情况。
除了递归思路,还有其他方式实现吗?
绝大多数可以用递归解决的问题,其实都可以用另一种数据结构来解决,这种数据结构就是栈。因为递归和栈都有回溯的特性。前序、中序、后序遍历的思路与递归一致,
java// 非递归中序遍历(栈实现)
void inOrderStack(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
TreeNode curr = root;
while (curr != null || !stack.isEmpty()) {
while (curr != null) {
stack.push(curr);
curr = curr.left;
}
curr = stack.pop();
System.out.print(curr.val + " ");
curr = curr.right;
}
}
广度优先遍历(BFS)
如果说深度优先遍历是在一个方向上“一头扎到底”,那么广度优先遍历则恰恰相反:先在各个方向上各走出1步,再在各个方向上走出第2步、第3步.…一直到各个方向全部走完
听起来有些抽象,下面让我们通过二叉树的层序遍历,来看一看广度优先是怎么回事。
层序遍历
二叉树按照从根节点到叶子节点的层次关系,一层一层横向遍历各个节点。
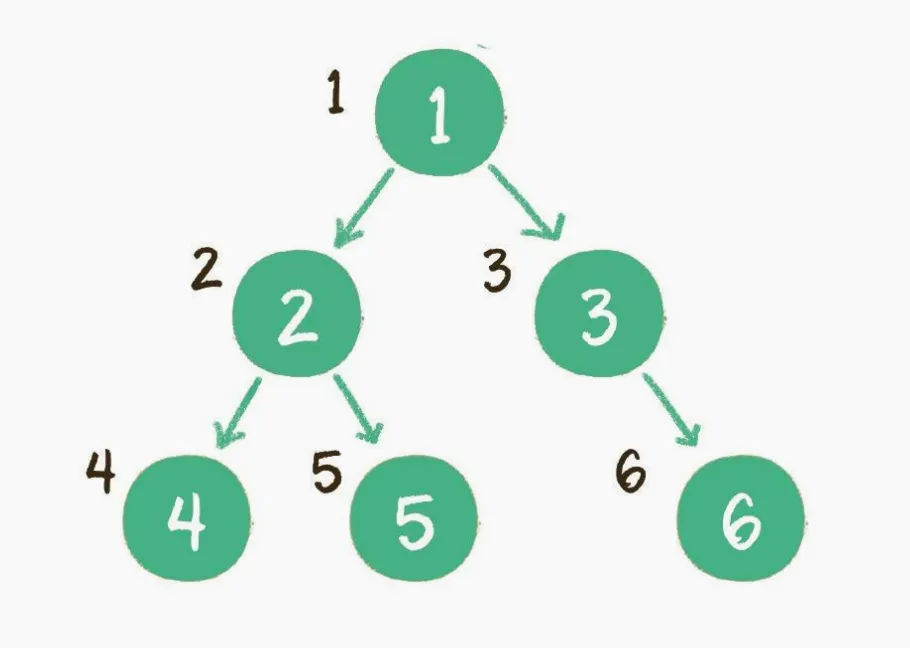
上图就是一个二叉树的层序遍历,每个节点左侧的序号代表该节点的输出顺序。
代码实现
二又树同一层次的节点之间是没有直接关联的,如何实现这种层序遍历呢?这里同样需要借助一个数据结构来辅助工作,这个数据结构就是队列。
javavoid levelOrder(TreeNode root) {
if (root == null) return;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int levelSize = queue.size();
for (int i = 0; i < levelSize; i++) {
TreeNode node = queue.poll();
System.out.print(node.val + " ");
if (node.left != null) queue.offer(node.left);
if (node.right != null) queue.offer(node.right);
}
System.out.println(); // 换行显示层级
}
}
二叉堆
二叉堆(Binary Heap) 是一种基于完全二叉树的数据结构,常用于实现优先队列。它分为两种类型:
- 最大堆(Max-Heap):最大堆的任何一个父节点的值,都大于或等于它左孩子或右孩子节点的值。
- 最小堆(Min-Heap):最小堆的任何一个父节点的值,都小于或等于它左孩子或右孩子节点的值。
二叉堆的根节点叫作堆顶。最大堆和最小堆的特点决定了:最大堆的堆顶是整个堆中的最大元素;最小堆的堆顶是整个堆中的最小元素。
最大堆中,父节点的值总是大于或等于其子节点的值,而最小堆则是父节点的值总是小于或等于子节点的值。这确保了堆顶元素是最大值或最小值,这对于优先队列来说非常有用,因为可以快速访问最高优先级的元素。
代码实现
完全二叉树结构
所有层级除最后一层外完全填满,最后一层节点向左对齐。这使得二叉堆可以用数组高效存储。
堆序性质
最大堆的根节点为最大值,最小堆的根节点为最小值。这一性质确保了高效访问和操作优先级元素。
数组表示
通过索引关系维护树结构(假设数组索引从 0 开始):
- 父节点索引:(i-1)/2
- 左子节点索引:2i+1
- 右子节点索引:2i+2
操作核心
基于堆的自我调整
- 插入节点:插入节点时,插入位置是二叉树的最后一个位置,通过节点"上浮"来确认最终位置
- 删除节点:与插入相反,则是将堆顶的节点删除,然后将堆最后一个节点补到堆顶,然后通过"下沉"操作来自动调整
- 构建二叉堆:将一个无序的完全二叉树调整为一个二叉堆,本质为将所有非叶子节点依次"下沉"
java// 最大堆
public class MaxHeap {
private int[] heap;
private int size;
private static final int DEFAULT_CAPACITY = 10;
public MaxHeap() {
heap = new int[DEFAULT_CAPACITY];
size = 0;
}
// 插入元素
public void insert(int value) {
if (size == heap.length) {
resize();
}
heap[size] = value;
siftUp(size);
size++;
}
// 删除堆顶元素
public int extractMax() {
if (size == 0) {
throw new IllegalStateException("Heap is empty");
}
int max = heap[0];
heap[0] = heap[size - 1];
size--;
siftDown(0);
return max;
}
// 上浮调整
private void siftUp(int index) {
int parent = (index - 1) / 2;
while (index > 0 && heap[index] > heap[parent]) {
swap(index, parent);
index = parent;
parent = (index - 1) / 2;
}
}
// 下沉调整
private void siftDown(int index) {
int maxIndex = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < size && heap[left] > heap[maxIndex]) {
maxIndex = left;
}
if (right < size && heap[right] > heap[maxIndex]) {
maxIndex = right;
}
if (index != maxIndex) {
swap(index, maxIndex);
siftDown(maxIndex);
}
}
// 构建堆(Heapify)
public void buildHeap(int[] array) {
heap = array;
size = array.length;
for (int i = (size - 1) / 2; i >= 0; i--) {
siftDown(i);
}
}
// 辅助方法:交换元素
private void swap(int i, int j) {
int temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
// 动态扩容
private void resize() {
int[] newHeap = new int[heap.length * 2];
System.arraycopy(heap, 0, newHeap, 0, heap.length);
heap = newHeap;
}
// 测试代码
public static void main(String[] args) {
MaxHeap heap = new MaxHeap();
heap.insert(3);
heap.insert(1);
heap.insert(4);
heap.insert(1);
heap.insert(5);
System.out.println(heap.extractMax()); // 输出 5
System.out.println(heap.extractMax()); // 输出 4
}
}
应用场景
- 优先队列:任务调度、Dijkstra算法中快速获取最小/最大值。
- 堆排序:时间复杂度 O(nlogn),原地排序。
- 合并K个有序链表:每次从堆中选取最小节点插入结果链表。
掌握
理解这些应用有助于更好地掌握堆的作用和重要性。
总结
- 二叉堆通过完全二叉树和数组结合,实现了高效的元素插入、删除和堆顶访问。
- 最大堆与最小堆根据需求选择,分别用于获取最大值或最小值。
- 堆排序和优先队列是二叉堆的典型应用,体现了其在算法中的核心作用。
二叉搜索树(Binary Search Tree, BST)
如果一颗二叉树符合“每一个节点的数据大于左节点切小于右节点”,那么这棵树就是一颗二叉搜索树
相关信息
二叉查找树、二叉搜索树和二叉排序树是同一数据结构的不同中文译名,三者本质上是相同的概念,没有实际区别。
核心特性
排序性质
- 左子树所有节点的值 < 根节点的值
- 右子树所有节点的值 > 根节点的值
- 左、右子树本身也是二叉搜索树
高效操作
利用排序特性,实现快速查找、插入、删除操作,理想情况下时间复杂度为 O(log n)。
中序遍历有序性
对二叉搜索树进行中序遍历,结果是一个升序序列。
代码实现
- 查找(Search)
java// 递归实现
public TreeNode search(TreeNode root, int target) {
if (root == null || root.val == target) {
return root;
}
if (target < root.val) {
return search(root.left, target);
} else {
return search(root.right, target);
}
}
- 插入(Insert)
javapublic TreeNode insert(TreeNode root, int val) {
if (root == null) {
return new TreeNode(val);
}
if (val < root.val) {
root.left = insert(root.left, val);
} else if (val > root.val) {
root.right = insert(root.right, val);
}
return root; // 重复值不插入
}
- 删除(Delete)
javapublic TreeNode delete(TreeNode root, int key) {
if (root == null) return null;
if (key < root.val) {
root.left = delete(root.left, key);
} else if (key > root.val) {
root.right = delete(root.right, key);
} else {
// 节点有一个子节点或无子节点
if (root.left == null) return root.right;
if (root.right == null) return root.left;
// 节点有两个子节点:用右子树最小值替代
TreeNode minNode = findMin(root.right);
root.val = minNode.val;
root.right = delete(root.right, minNode.val);
}
return root;
}
private TreeNode findMin(TreeNode node) {
while (node.left != null) {
node = node.left;
}
return node;
}
二叉搜索树的退化问题
二叉搜索树的缺点是无法永远保持在最佳状态,若插入的数据有序(如连续递增或递减),当前二叉树的结构就会变为斜二叉树,从而使树的高度增加,二叉搜索树会退化为链表,导致操作效率从 O(log n) 降至 O(n)。,因此二叉树不适用于数据经常变动(插入、删除)的情况。
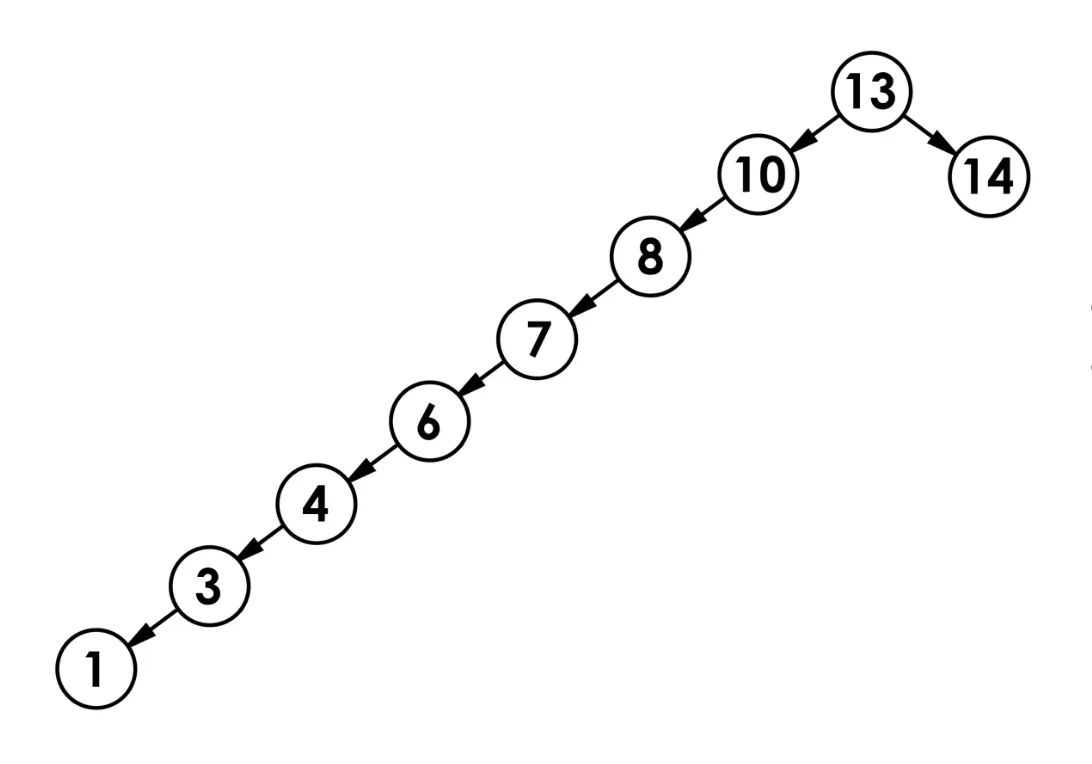
解决方案:使用平衡二叉搜索树(如AVL树、红黑树),通过旋转操作维持树高平衡。如Java的 TreeMap 基于红黑树来保证稳定性能。
平衡树(AVL树)
平衡树是一种通过约束节点分布来保持树结构平衡的数据结构,目的是解决普通二叉搜索树(BST)在极端情况下退化为链表的性能问题。通过动态调整节点位置,会对二叉树的高度做出一些调整,从而让整个树的高度随时维持平衡,确保所有操作(查找、插入、删除)的时间复杂度稳定在 O(log n)。
java// AVL树代码实现
class AVLNode {
int val;
int height; // 节点高度
AVLNode left;
AVLNode right;
AVLNode(int val) {
this.val = val;
this.height = 1; // 新节点初始高度为1
}
}
平衡标准
是一棵二叉搜索树 任意节点的左右子树高度差 ≤ 1
平衡因子 BF(Balance Factor)
定义
左子树和右子树高度差
计算
左子树高度 - 右子树高度的值
java// 获取节点高度
private int height(AVLNode node) {
return (node == null) ? 0 : node.height;
}
// 计算平衡因子
private int getBalanceFactor(AVLNode node) {
if (node == null) return 0;
return height(node.left) - height(node.right);
}
旋转的时机
一般来说 BF 的绝对值大于 1,平衡树二叉树就失衡,需要「旋转」纠正
距离插入节点最近的,并且 BF 的绝对值大于 1 的节点为根节点的子树,「旋转」纠正只需要纠正「最小不平衡子树」即可
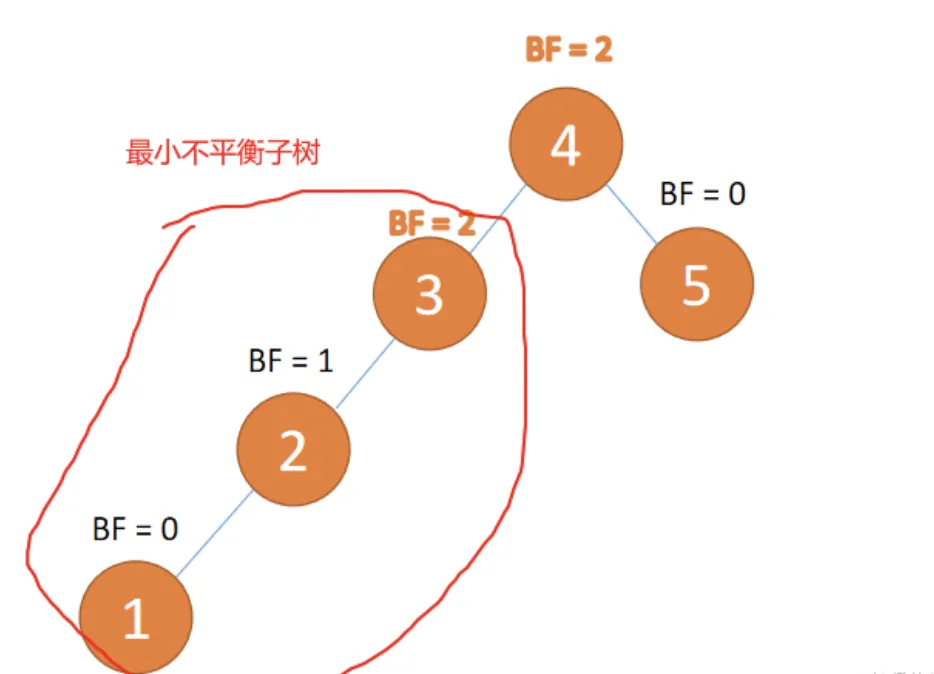
2 种「旋转」方式
左旋
- 让旧根节点为新根节点的左子树
- 让新根节点的左子树(如果存在)为旧根节点的右子树
右旋
- 让旧根节点为新根节点的右子树
- 让新根节点的右子树(如果存在)为旧根节点的左子树
4 种「旋转」操作
左左型(LL):插入左孩子的左子树,「右旋」
第三个节点「1」插入的时候,左子树 LL 型失衡,需要「右旋」,根节点顺时针旋转
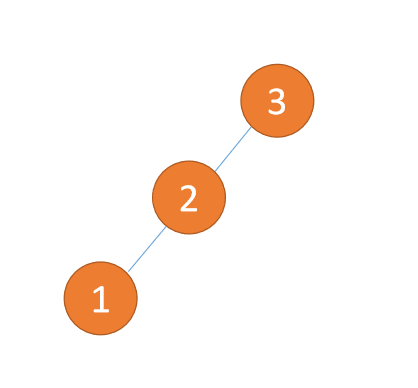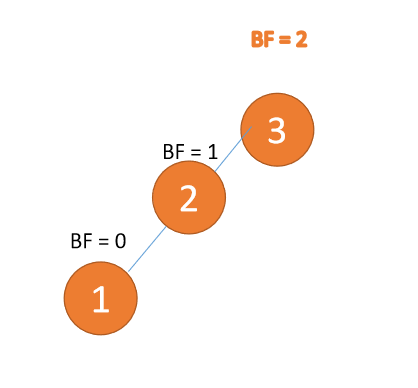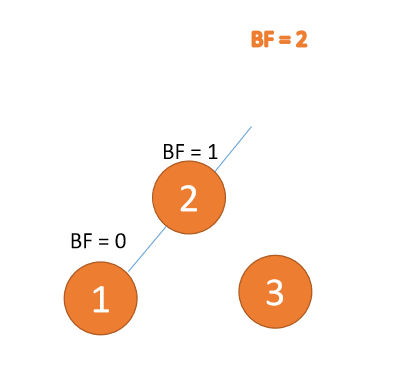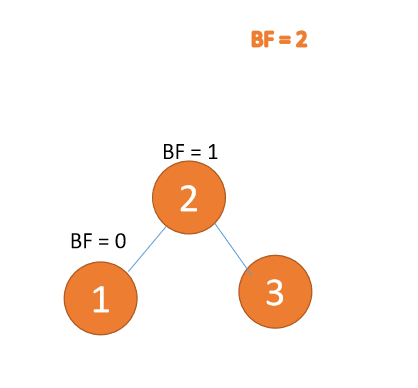
「右旋」:
- 旧根节点(节点 3)为新根节点(节点 2)的右子树
- 新根节点的 右子树(如果存在)为旧根节点的左子树
java// 右旋操作(修复左左失衡)
private AVLNode rightRotate(AVLNode y) {
// 获取失衡节点的左子节点
AVLNode x = y.left;
AVLNode T3 = x.right;
// 旋转操作
x.right = y;
y.left = T3;
// 更新高度(必须先更新子节点高度)
y.height = Math.max(height(y.left), height(y.right)) + 1;
x.height = Math.max(height(x.left), height(x.right)) + 1;
return x; // 返回新的根节点
}
右右型(RR):插入右孩子的右子树,「左旋」
第三个节点「3」插入的 时候,BF(1)=-2 BF(2)=-1,RR 型失衡,左旋,根节点逆时针旋转
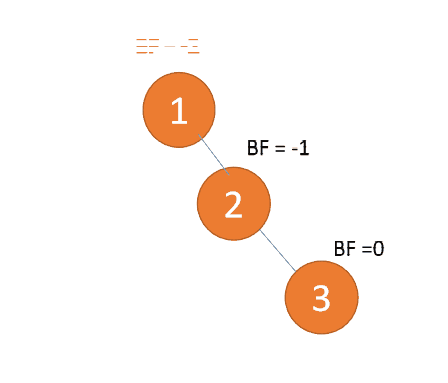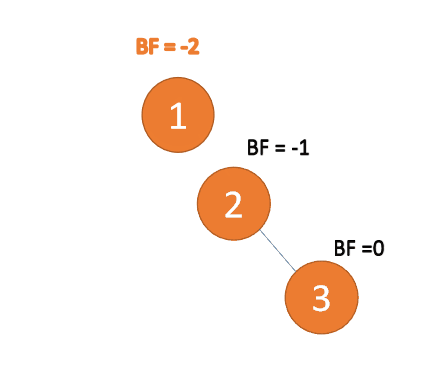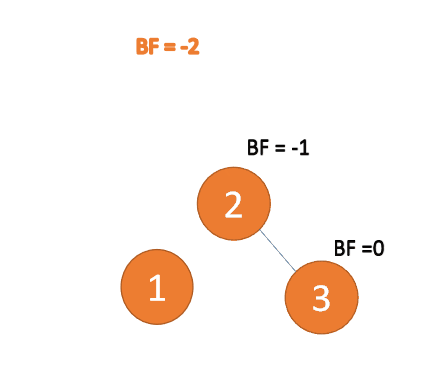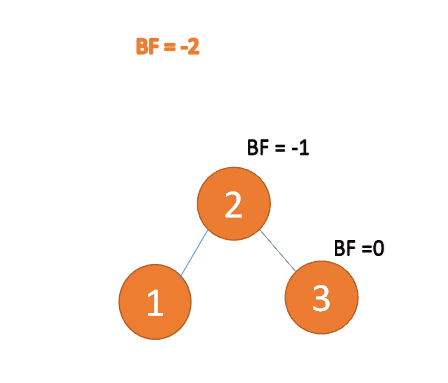
「左旋」:
- 旧根节点(节点 1)为新根节点(节点 2)的左子树
- 新根节点的左子树(如果存在)为旧根节点的右子树
java// 左旋操作(修复右右失衡)
private AVLNode leftRotate(AVLNode x) {
// 获取失衡节点的右子节点
AVLNode y = x.right;
AVLNode T2 = y.left;
// 旋转操作
y.left = x;
x.right = T2;
// 更新高度
x.height = Math.max(height(x.left), height(x.right)) + 1;
y.height = Math.max(height(y.left), height(y.right)) + 1;
return y; // 返回新的根节点
}
左右型(LR):插入左孩子的右子树,先「左旋」,再「右旋」
第三个节点「3」插入的 时候,BF(3)=2 BF(1)=-1 LR 型失衡,先「左旋」再「右旋」
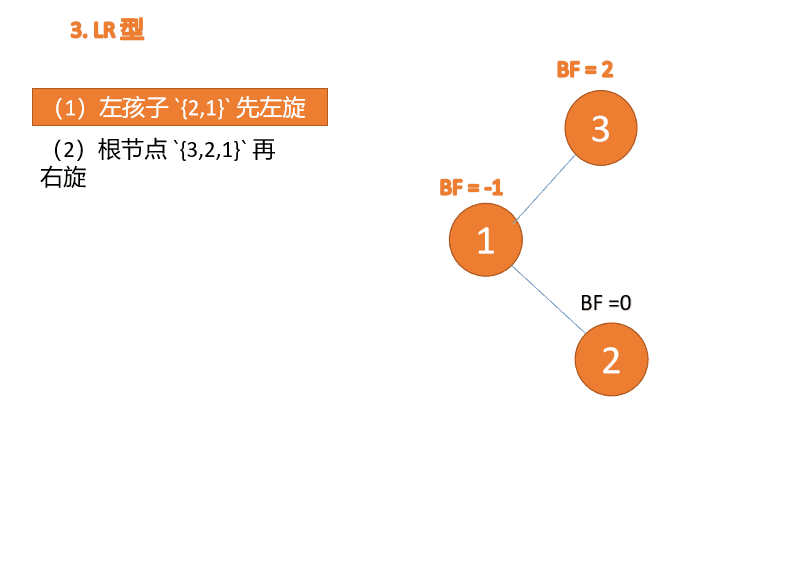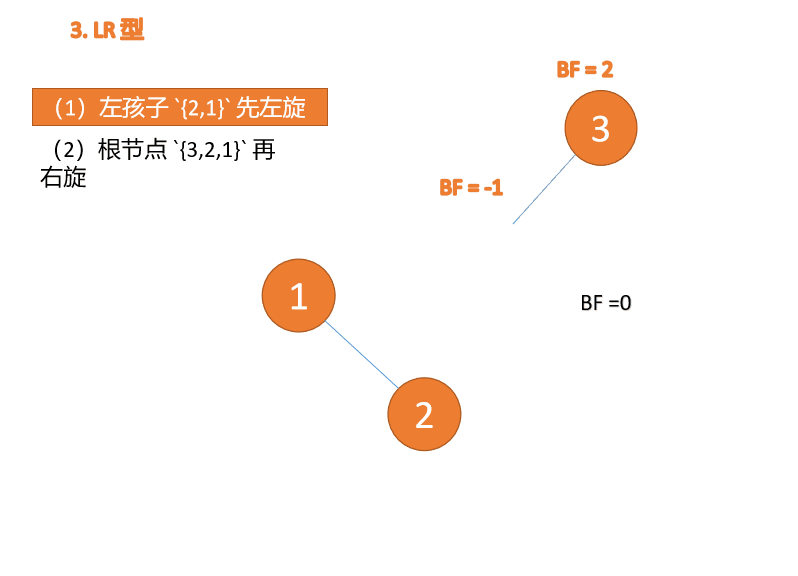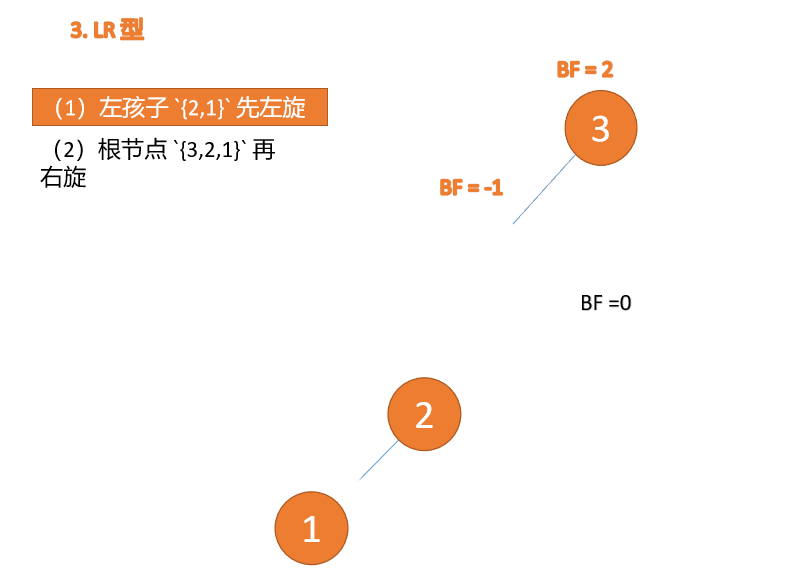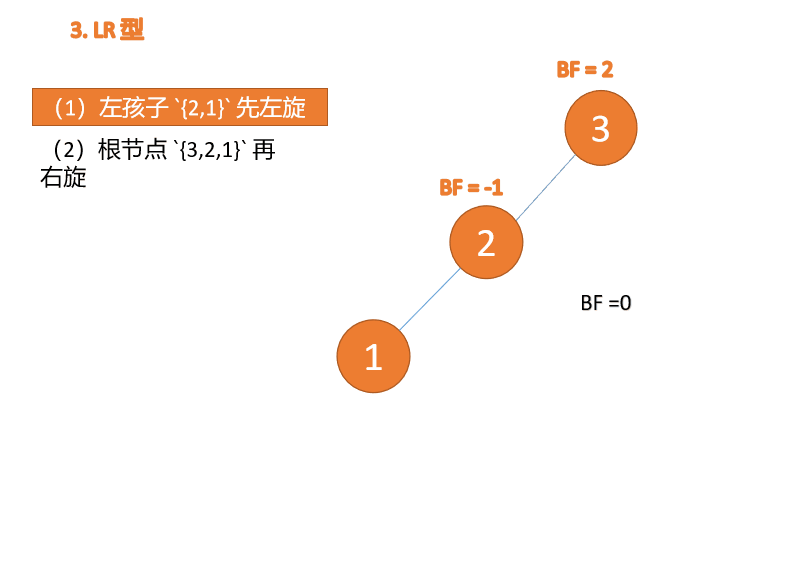
「左旋」:
- 旧根节点(节点 1)为新根节点(节点 2)的左子树
- 新根节点的左子树(如果存在)为旧根节点的右子树
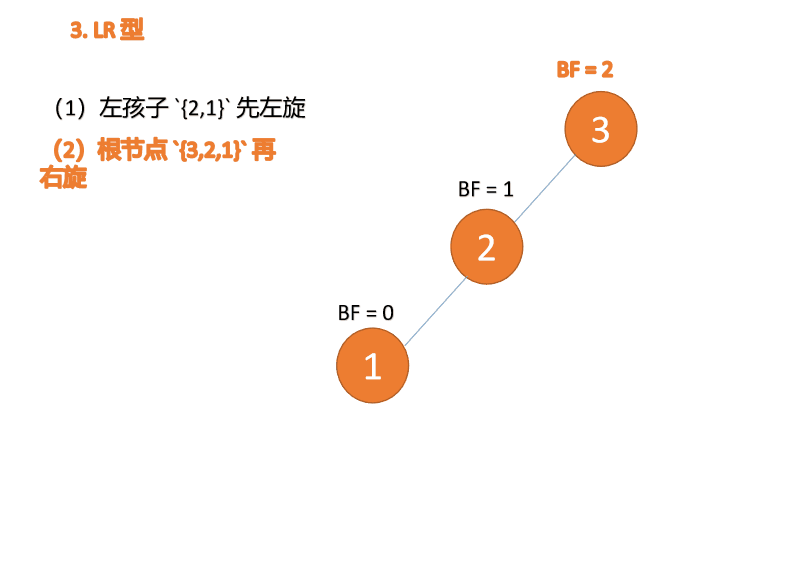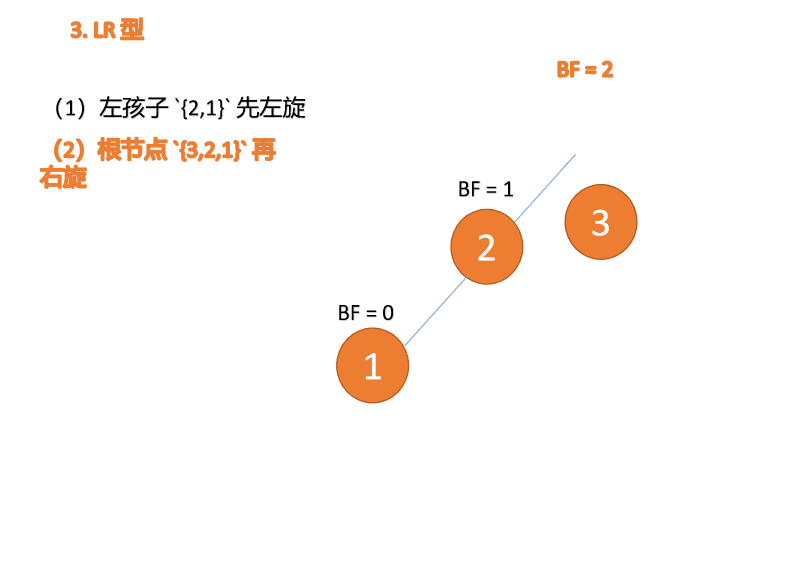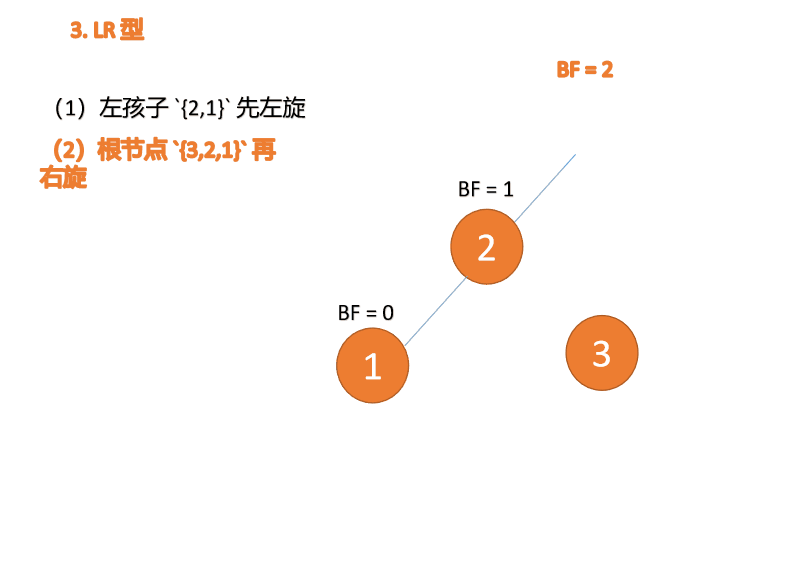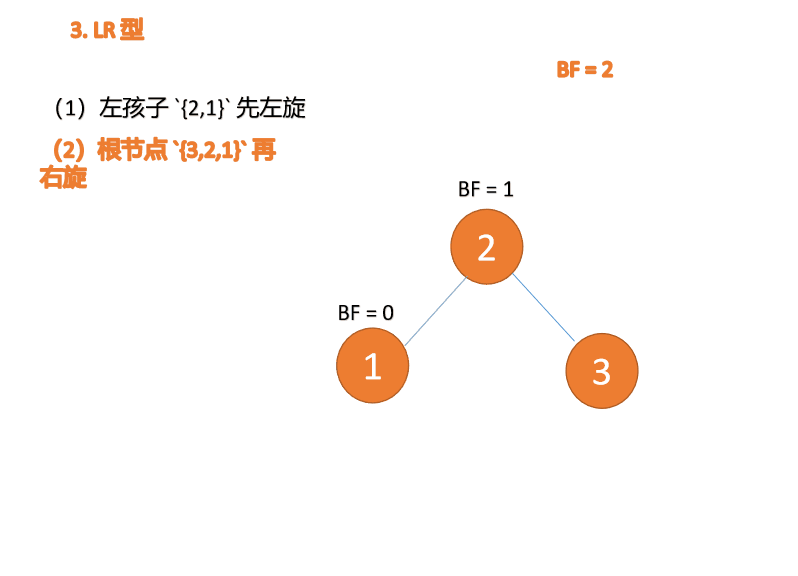
「右旋」:
-
旧根节点(节点 3)为新根节点(节点 2)的右子树
-
新根节点的 右子树(如果存在)为旧根节点的左子树
java// 修复左右失衡
private AVLNode lrRotate(AVLNode node) {
// 1. 对左子节点左旋
node.left = leftRotate(node.left);
// 2. 对当前节点右旋
return rightRotate(node);
}
右左型(RL):插入右孩子的左子树,先「右旋」,再「左旋」
第三个节点「1」插入的 时候,BF(1)=-2 BF(3)=1 RL 型失衡,先「右旋」再「左旋」
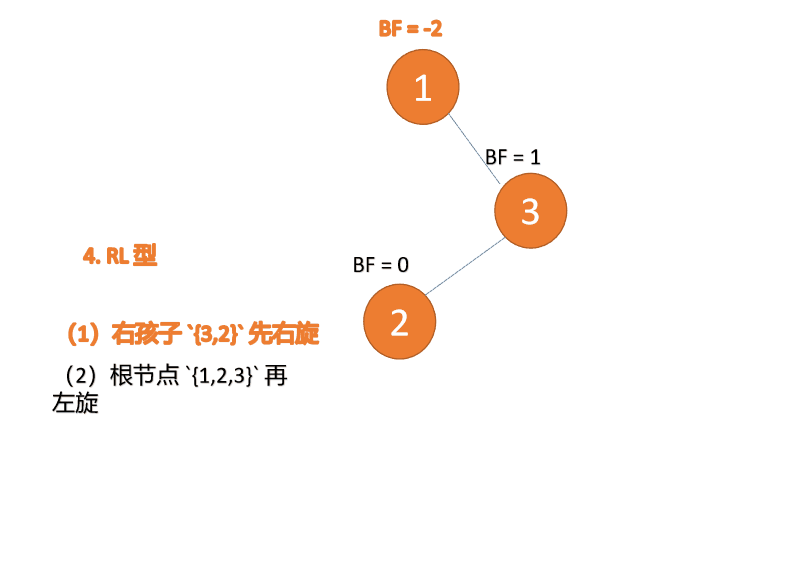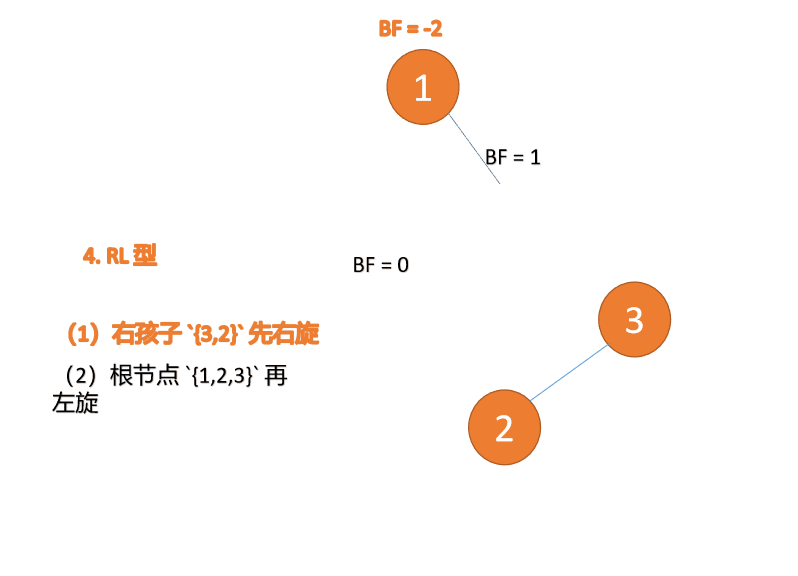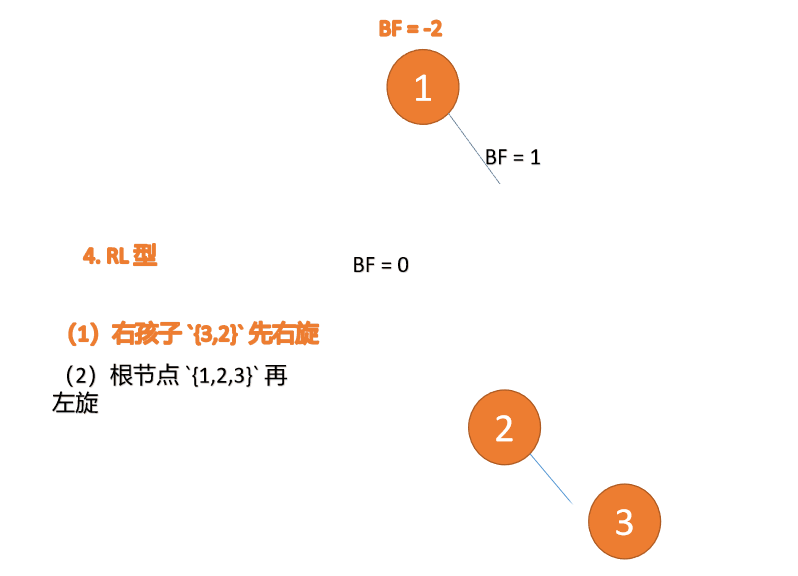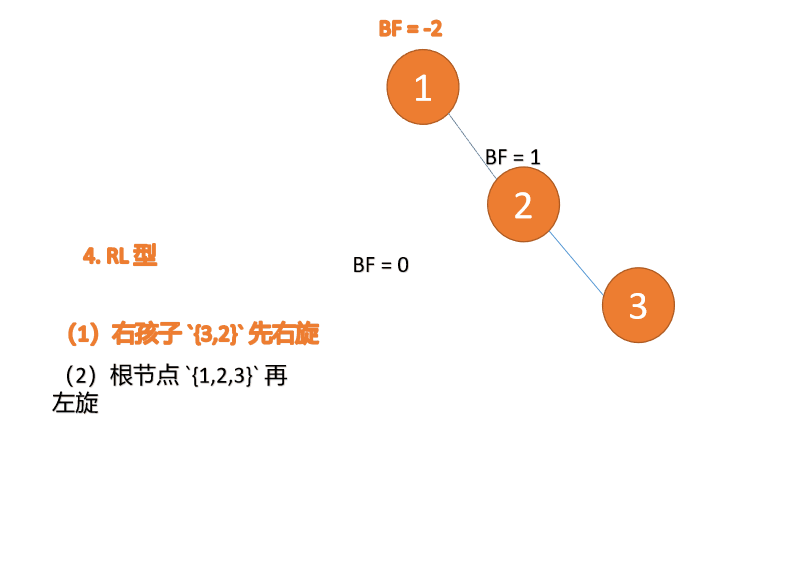
「右旋」:
- 旧根节点(节点 3)为新根节点(节点 2)的右子树
- 新根节点的 右子树(如果存在)为旧根节点的左子树
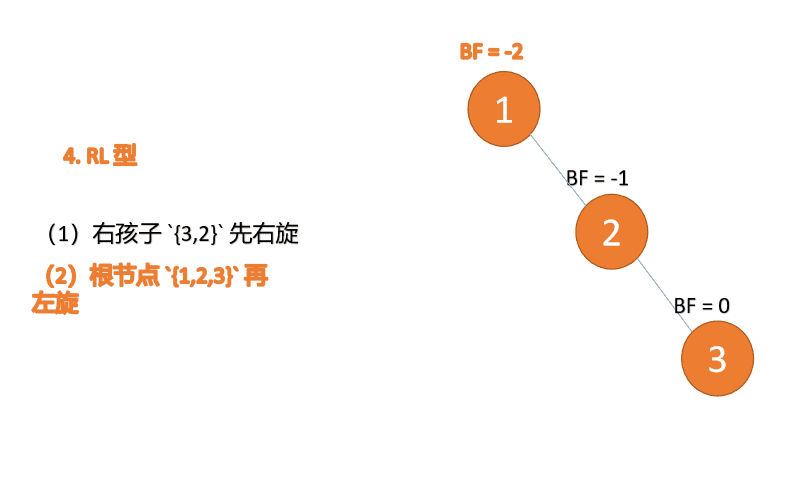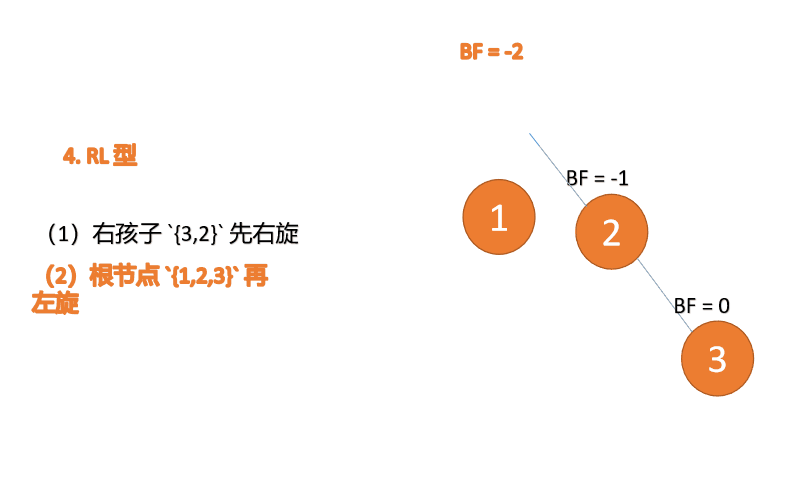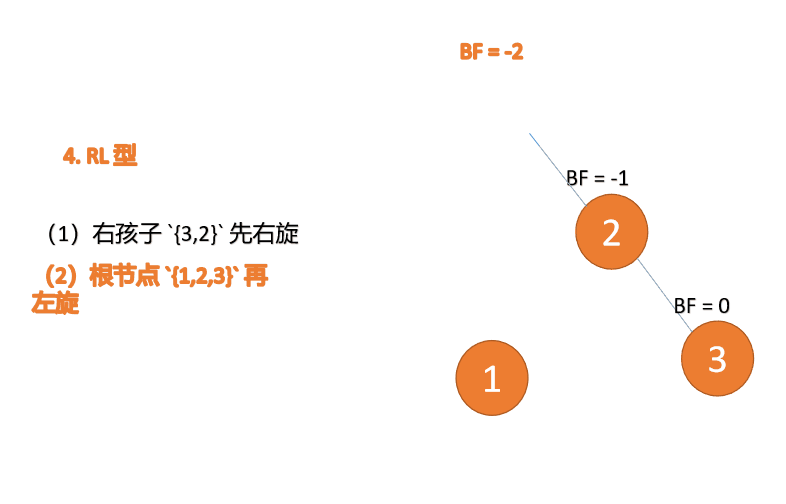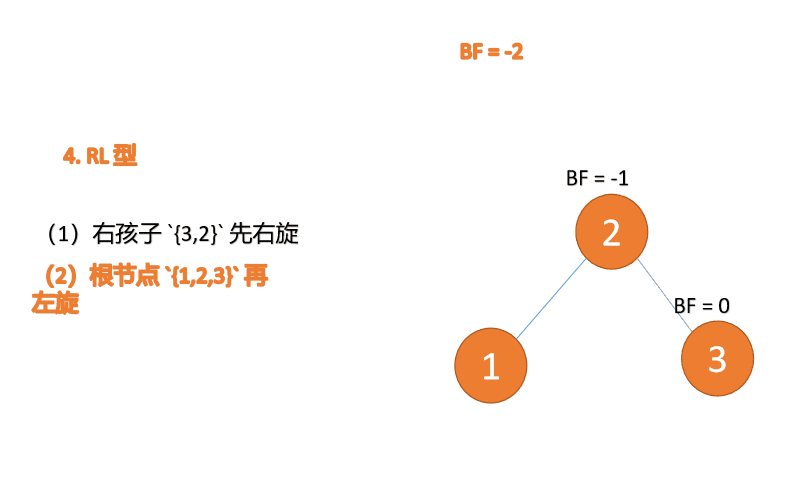
「左旋」:
- 旧根节点(节点 1)为新根节点(节点 2)的左子树
- 新根节点的左子树(如果存在)为旧根节点的右子树
java// 修复右左失衡
private AVLNode rlRotate(AVLNode node) {
// 1. 对右子节点右旋
node.right = rightRotate(node.right);
// 2. 对当前节点左旋
return leftRotate(node);
}
插入的代码实现
javapublic class AVLTree {
private AVLNode root;
// 插入入口方法
public void insert(int val) {
root = insert(root, val);
}
private AVLNode insert(AVLNode node, int val) {
// 1. 标准BST插入
if (node == null) return new AVLNode(val);
if (val < node.val) {
node.left = insert(node.left, val);
} else if (val > node.val) {
node.right = insert(node.right, val);
} else {
return node; // 不允许重复值
}
// 2. 更新高度
node.height = 1 + Math.max(height(node.left), height(node.right));
// 3. 计算平衡因子
int balance = getBalanceFactor(node);
// 4. 根据失衡类型旋转
// 左左失衡
if (balance > 1 && val < node.left.val) {
return rightRotate(node);
}
// 右右失衡
if (balance < -1 && val > node.right.val) {
return leftRotate(node);
}
// 左右失衡
if (balance > 1 && val > node.left.val) {
return lrRotate(node);
}
// 右左失衡
if (balance < -1 && val < node.right.val) {
return rlRotate(node);
}
return node;
}
public static void main(String[] args) {
AVLTree tree = new AVLTree();
// 测试左左失衡(插入3→2→1)
tree.insert(3);
tree.insert(2);
tree.insert(1); // 触发右旋
// 测试右右失衡(插入1→2→3)
tree.insert(1);
tree.insert(2);
tree.insert(3); // 触发左旋
// 测试左右失衡(插入3→1→2)
tree.insert(3);
tree.insert(1);
tree.insert(2); // 触发左右旋
// 测试右左失衡(插入1→3→2)
tree.insert(1);
tree.insert(3);
tree.insert(2); // 触发右左旋
}
}
左左失衡(右旋)
失衡前: 3 / 2 / 1 右旋后: 2 / \ 1 3
右右失衡(左旋)
失衡前: 1 \ 2 \ 3 左旋后: 2 / \ 1 3
左右失衡(左旋、右旋)
失衡前: 3 / 1 \ 2 左旋后: 3 / 2 / 1 右旋后: 2 / \ 1 3
右左失衡(右旋、左旋)
失衡前: 1 \ 3 / 2 右旋后: 1 \ 2 \ 3 左旋后: 2 / \ 1 3
总结
- 左左/右右失衡:直接通过单次旋转(右旋/左旋)修复。
- 左右/右左失衡:需要两次旋转(先子节点旋转,再父节点旋转)修复。
- 平衡因子计算:通过节点高度差判断失衡类型。
- 时间复杂度:所有旋转操作均为 O(1),插入整体复杂度 O(log n)。
实际应用中,每次插入/删除后都需要检查平衡因子并执行相应旋转,确保树始终保持平衡状态。
图
图的组成
图论(Graph Theory)是离散数学的一个分支,图(Graph)是由点集合和这些点之间的连线组成,其中点被称为:顶点(Vertex/Node/Point),点与点之间的连线则被称为:边(Edge/Arc/Link)。
图是由顶点(Vertex)和边(Edge)构成,边表示顶点间的关系。记为,G = (V, E)。
注意
值得注意的是,图的顶点集合不能为空,但边的集合可以为空,通俗的讲,一张图,没有点不行,没有边可以,大不了点与点之间不相连。
稀疏图和稠密图
- 稀疏图(Sparse Graph):边的数目相对较少(远小于 n x (n-1))的图称为稀疏图。
- 稠密图(Dense Graph):边的数目相对较多的图称为稠密图。
关键术语:
- 度(Degree):顶点连接的边数(无向图);入度和出度(有向图)。
- 路径与环:顶点间的连通路径及闭合路径
图的分类
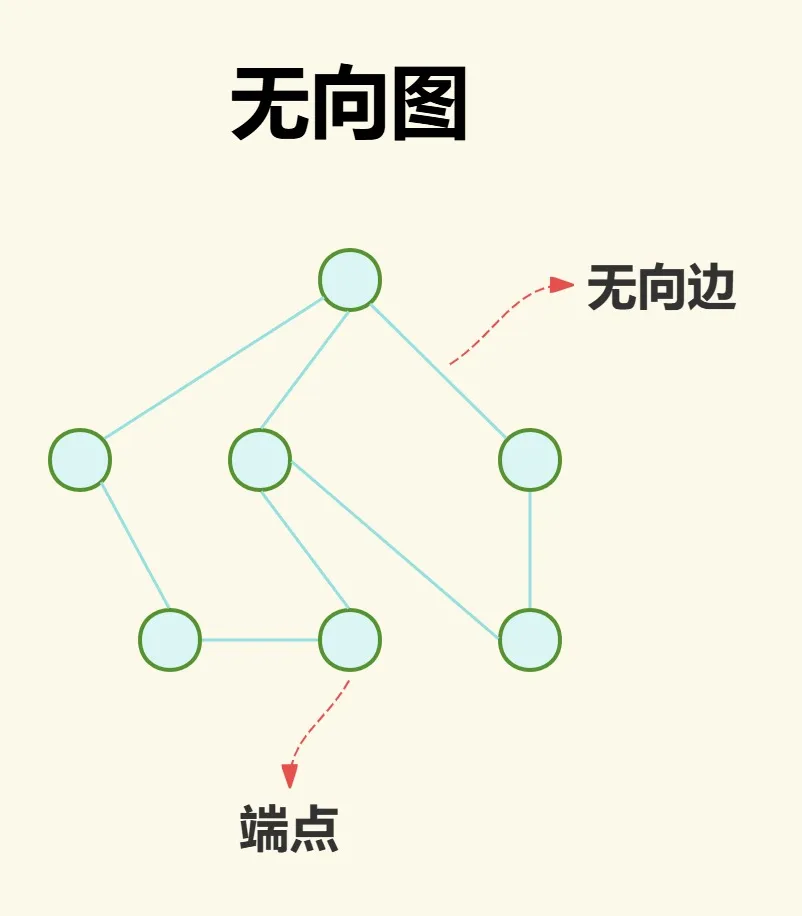
无向图
无向图就是边无方向性(如A-B等价于B-A),即两个点之间没有方向,没有顺序之分,这样的边叫作无向边,也简称边。其中点也叫作端点。
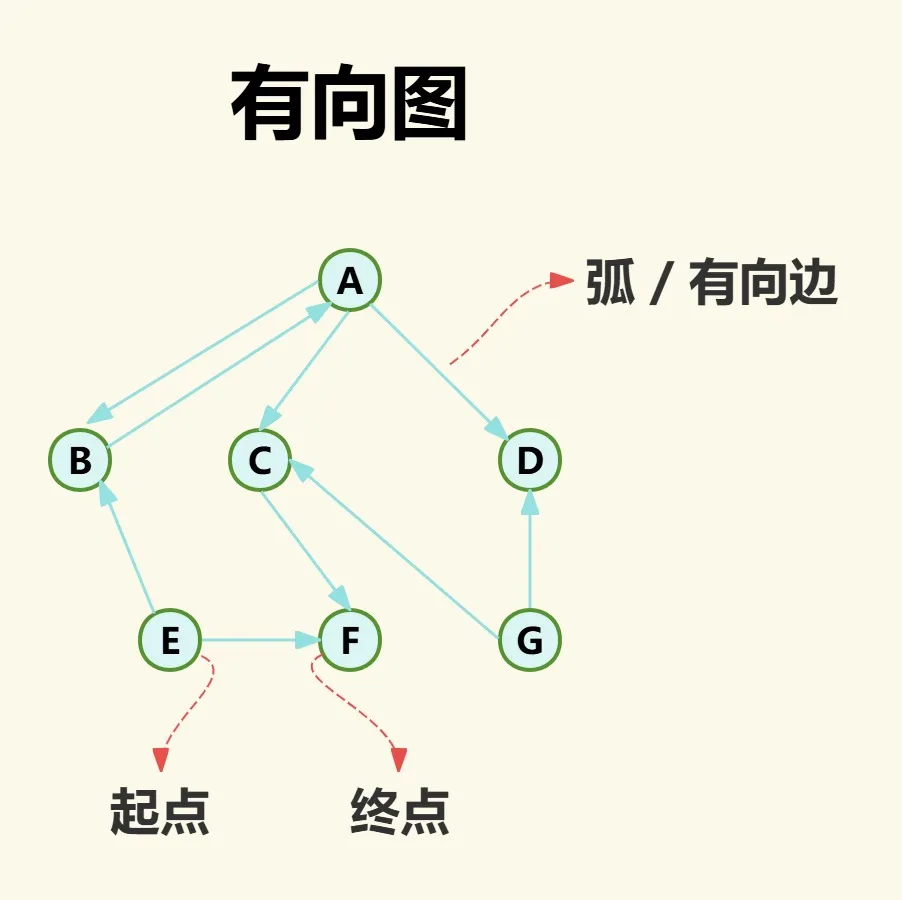
有向图
有向图是指边具有方向性(如A→B),也就代表边所连接的两点有顺序之分,其中一个为起点,则另一个则为终点,而这样的边就叫作有向边或弧,起点和终点也叫端点.
其中同一个点既可以是起点,也可以是终点。
对于任何图,与一个点关联的所有边数称为该点的度。
而对于有向图来说,以一个点为起点的边数称为该的点出度,以一个点为终点的边数称为该点的入度。
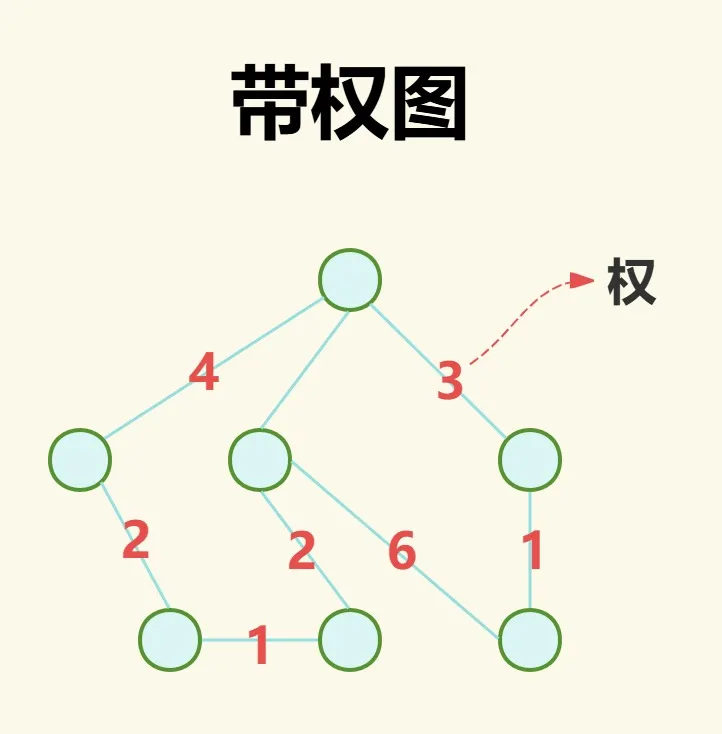
加权图
加权图指每个边带有权重值(如路径长度或成本)。代表边连接的两点关系的强弱、远近。同时权只是代表边的权重,并不代表边的方向,因此无论无边图还是有边图都可以是加权图。
图的数据存储方式
图的存储可以通过顺序存储结构和链式存储结构来实现。其中顺序存储结构包括:邻接矩阵和边集数组。链式存储结构包括:邻接表、链式前向星、十字链表和邻接多重表。
接下来我们来介绍两种常用的图存储结构:邻接矩阵与邻接表。
邻接矩阵
邻接矩阵就是用一个二维数组来存储任意两点之间的关系,其中行列索引表示点,而行列索引所在的位置的值表示两点关系,其中两点关系可以用以下数值表示:
- 0:表示两点之间没有边;
- 1:表示两点之间有边;
- 权值:表示两点之间边的权值;
如果图存在n个点,则可以用n x n的二维数组来表示图,下面我们来看看常见图的表示方式。
无向图
对于无向图,如果点A与点B有边,则[A,B]与[B,A]都为1,否则都为0,因此无向图的邻接矩阵是对称的,如下图:
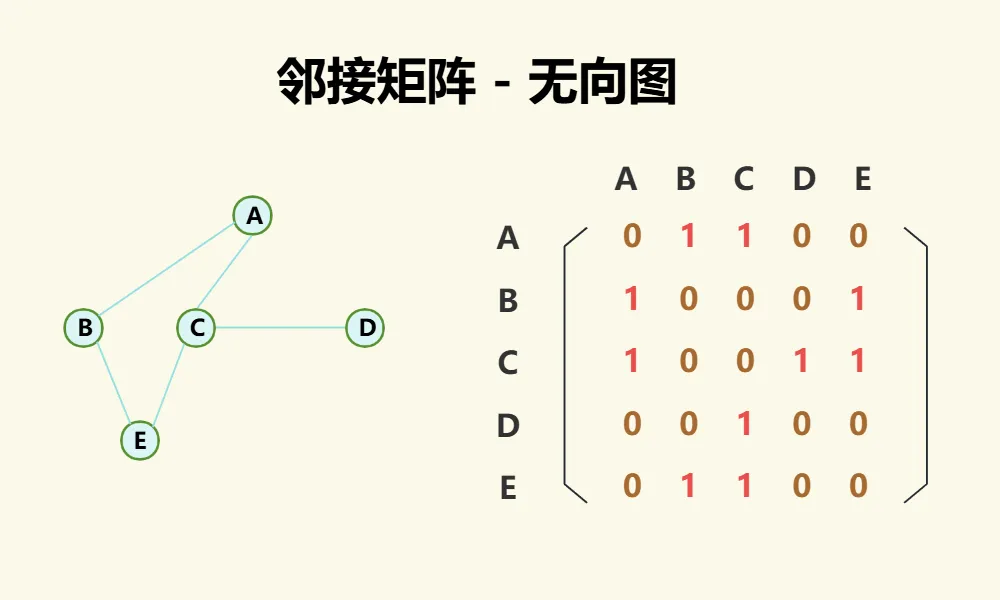
【邻接矩阵-无向图】代码实现
javapublic class UndirectedMatrixGraph {
private int[][] matrix; // 邻接矩阵
private int vertexCount; // 顶点数量
public UndirectedMatrixGraph(int vertexCount) {
this.vertexCount = vertexCount;
matrix = new int[vertexCount][vertexCount];
}
// 添加边(无权重)
public void addEdge(int i, int j) {
if (i >= 0 && i < vertexCount && j >= 0 && j < vertexCount) {
matrix[i][j] = 1; // 无向图双向标记
matrix[j][i] = 1;
}
}
// 打印邻接矩阵
public void printMatrix() {
for (int[] row : matrix) {
System.out.println(Arrays.toString(row));
}
}
public static void main(String[] args) {
UndirectedMatrixGraph g = new UndirectedMatrixGraph(4);
g.addEdge(0, 1); // 边 0-1
g.addEdge(0, 2); // 边 0-2
g.printMatrix();
}
}
有向图
对于有向图,则可以通过把行索引当作边的起点,把列当作边的终点,来表示方向,比如[A,B]为1,而[B,A]为0,如下图:
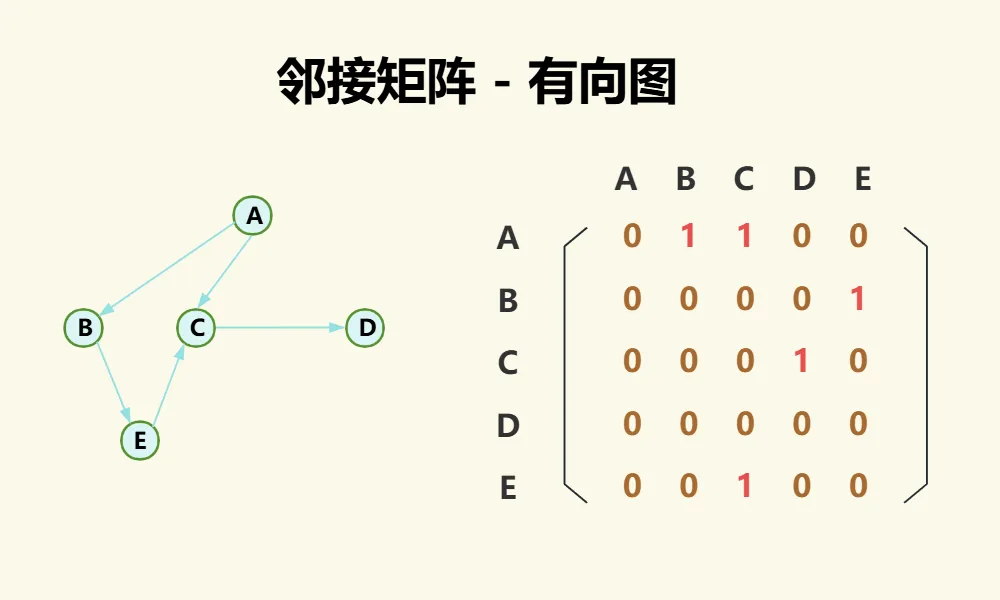
对于有向图,我们可以发现关于点的度有以下特性:
- 点的出度就是第i行元素之和;
- 点的入度就是第i列元素之和;
- 点的度就是第i行元素之和 + 第i列元素之和;
【邻接矩阵-有向图】代码实现
javapublic class DirectedMatrixGraph {
private int[][] matrix;
private int vertexCount;
public DirectedMatrixGraph(int vertexCount) {
this.vertexCount = vertexCount;
matrix = new int[vertexCount][vertexCount];
}
// 添加有向边 i → j
public void addEdge(int i, int j) {
if (i >= 0 && i < vertexCount && j >= 0 && j < vertexCount) {
matrix[i][j] = 1;
}
}
// 打印方法同上(略)
}
加权图
对于加权图,本质上和无向图与有向图相同,只是存储的值有所差别,如果两点之间有边则直接存权值,如果两点之间无边则存一个特殊值(如0、无穷),如果可以保证权值中不存在0,可以用0,否则要选一个其他特殊值,如下图:
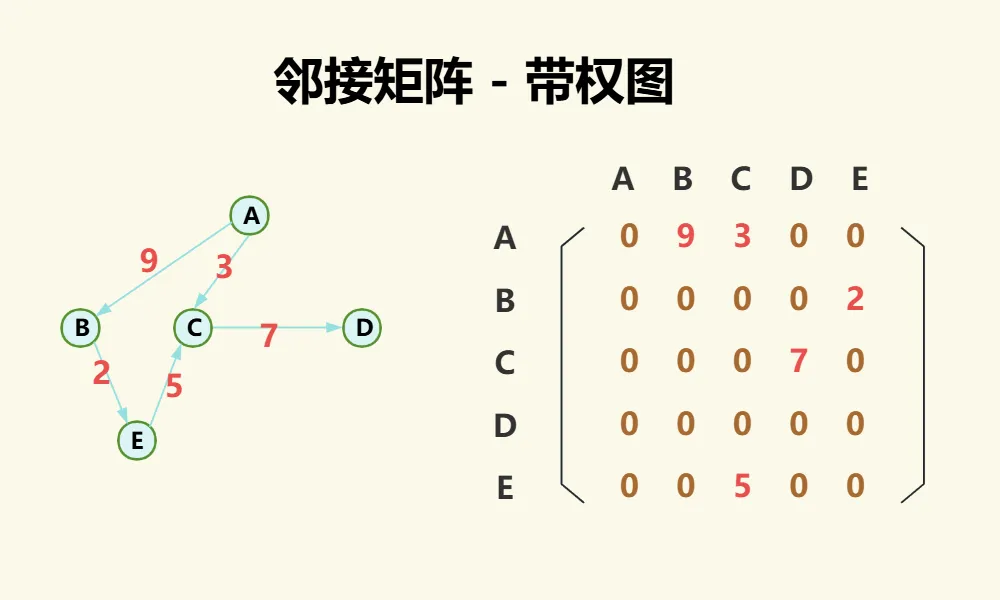
【邻接矩阵-加权图】代码实现
javapublic class WeightedMatrixGraph {
private int[][] matrix;
private int vertexCount;
public WeightedMatrixGraph(int vertexCount) {
this.vertexCount = vertexCount;
matrix = new int[vertexCount][vertexCount]; // 0表示无连接
}
// 添加带权重的边
public void addEdge(int i, int j, int weight) {
if (i >= 0 && i < vertexCount && j >= 0 && j < vertexCount) {
matrix[i][j] = weight;
matrix[j][i] = weight; // 无向图需双向设置
}
}
// 打印方法同上(略)
}
优缺点
优点:
- 简单直观:实现简单,易于理解,尤其适合小型图。
- 快速查找:便于判断两点之间是否有边,以及各点的度。
缺点:
- 空间浪费:空间复杂度高为O(n^2),对于稀疏图,许多元素为零,造成空间浪费。
- 不易扩展:不便于插入和删除点,需要更新整个矩阵,时间复杂度高为O(n)。
邻接表
对于邻接矩阵空间浪费以及不易扩展的问题,发展出了另一种链式存储方式——「邻接表」。
邻接表的存储思想和前面章节介绍的散列的链式存储很像。首先我们用一个数组存储所有的点,而每个点元素又作为单链表头,其后继节点则存储与头节点相邻的点元素。
无向图
如下图,图中所有点都存储在数组中,而与其相邻的点存储在其后面的链表中。
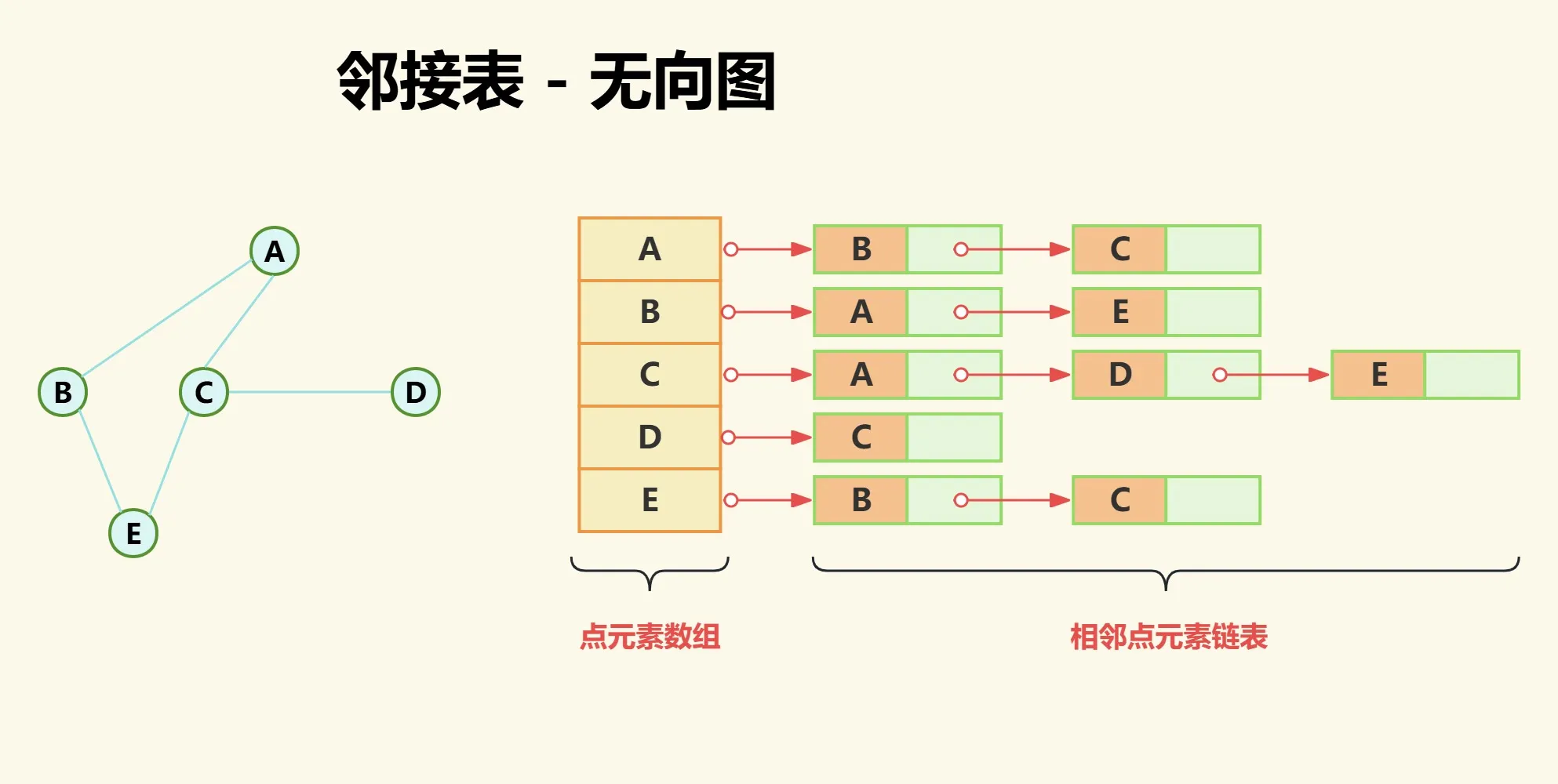
- 点A相邻的点为点B和点C;
- 点C相邻的点为点A、点D和点E;
- 点D相邻的点为点C;
【邻接表-无向图】代码实现
javapublic class UndirectedListGraph {
private List<List<Integer>> adjList;
private int vertexCount;
public UndirectedListGraph(int vertexCount) {
this.vertexCount = vertexCount;
adjList = new ArrayList<>();
for (int i = 0; i < vertexCount; i++) {
adjList.add(new LinkedList<>());
}
}
// 添加边
public void addEdge(int i, int j) {
if (i >= 0 && i < vertexCount && j >= 0 && j < vertexCount) {
adjList.get(i).add(j); // 双向添加
adjList.get(j).add(i);
}
}
// 打印邻接表
public void printAdjList() {
for (int i = 0; i < vertexCount; i++) {
System.out.print(i + " -> ");
System.out.println(adjList.get(i));
}
}
public static void main(String[] args) {
UndirectedListGraph g = new UndirectedListGraph(4);
g.addEdge(0, 1); // 边 0-1
g.addEdge(0, 2); // 边 0-2
g.printAdjList();
}
}
有向图
与无向图不同的是有向图链表中存储的不是所有相邻的点,而是存储有方向的点,即以数组中的点为起的终点元素。
通过下图可以发现,邻接表对于有向图可以很直观的表示出某个点的出度,但是对于入度获取就很麻烦。
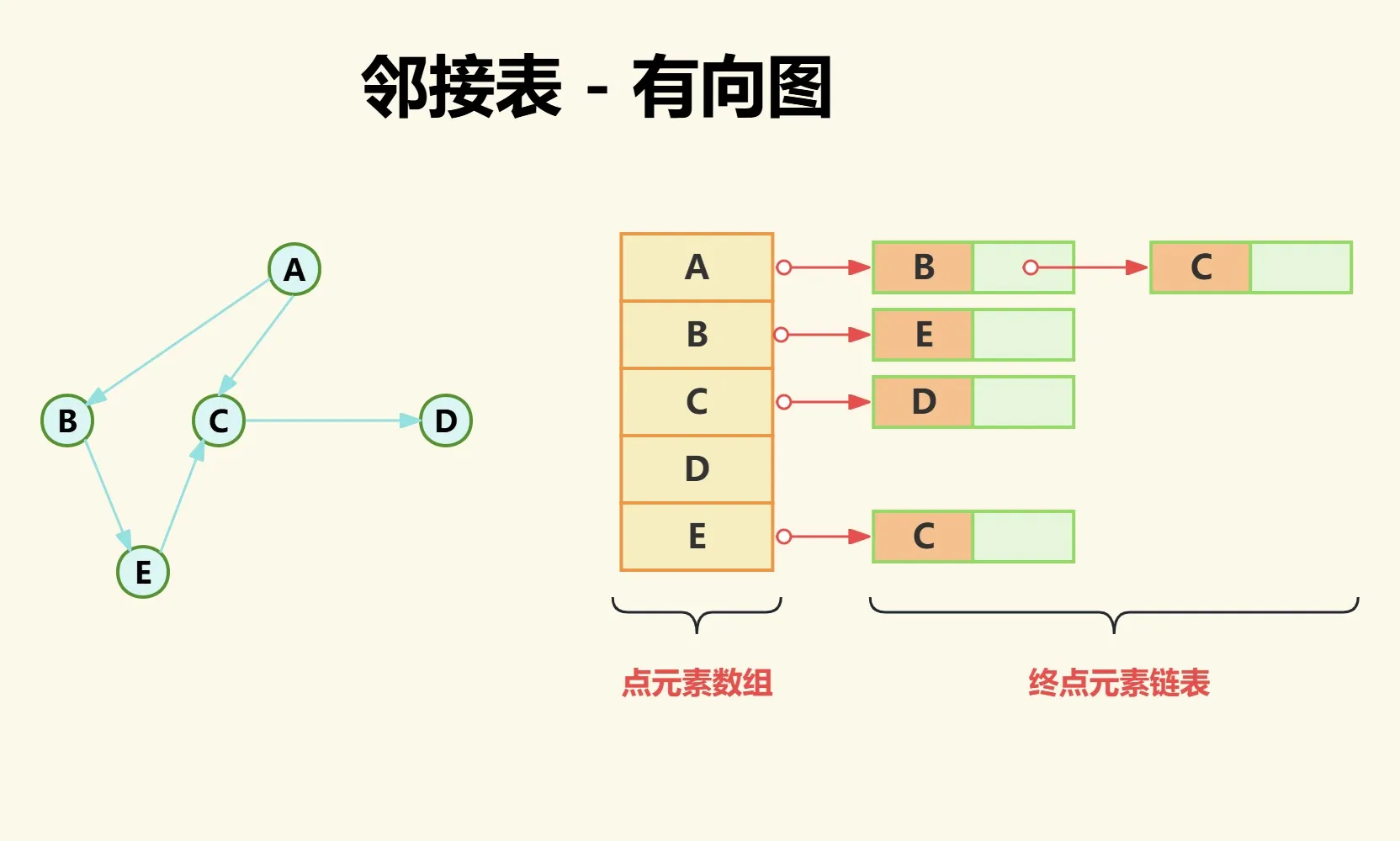
- 点A为起点的终点为点B和点C;
- 点B为起点的终点为点E;
- 点D为起点的终点不存在;
【邻接表-有向图】代码实现
javapublic class DirectedListGraph {
private List<List<Integer>> adjList;
private int vertexCount;
public DirectedListGraph(int vertexCount) {
this.vertexCount = vertexCount;
adjList = new ArrayList<>();
for (int i = 0; i < vertexCount; i++) {
adjList.add(new LinkedList<>());
}
}
// 添加有向边 i → j
public void addEdge(int i, int j) {
if (i >= 0 && i < vertexCount && j >= 0 && j < vertexCount) {
adjList.get(i).add(j);
}
}
// 打印方法同上(略)
}
加权图
加权图与无向图和有向图相比,只需要在元素中多加一个权重属性即可。
【邻接表-加权图】代码实现
java// 定义边类(存储目标顶点和权重)
class Edge {
int target;
int weight;
Edge(int target, int weight) {
this.target = target;
this.weight = weight;
}
@Override
public String toString() {
return "(" + target + ", " + weight + ")";
}
}
public class WeightedListGraph {
private List<List<Edge>> adjList;
private int vertexCount;
public WeightedListGraph(int vertexCount) {
this.vertexCount = vertexCount;
adjList = new ArrayList<>();
for (int i = 0; i < vertexCount; i++) {
adjList.add(new LinkedList<>());
}
}
// 添加带权重的边(无向)
public void addEdge(int i, int j, int weight) {
if (i >= 0 && i < vertexCount && j >= 0 && j < vertexCount) {
adjList.get(i).add(new Edge(j, weight));
adjList.get(j).add(new Edge(i, weight));
}
}
// 打印邻接表
public void printAdjList() {
for (int i = 0; i < vertexCount; i++) {
System.out.print(i + " -> ");
System.out.println(adjList.get(i));
}
}
public static void main(String[] args) {
WeightedListGraph g = new WeightedListGraph(4);
g.addEdge(0, 1, 5); // 边 0-1 权重5
g.addEdge(0, 2, 3); // 边 0-2 权重3
g.printAdjList();
}
}
优缺点
优点:
- 节省空间:时间复杂度相对较低为O(m+n),m为点数量,n为边数量,对于稀疏图存储效率更高;
- 操作灵活:插入和删除点操作方便,时间复杂度为O(1);
- 出度易取:对于有向图获取某个点的出度非常方便,只需要找到这个点所在的数组元素位置,然后获取其链表中的元素个数即可;
缺点:
- 不便查找:判断两点之间是否有边的时间复杂度为O(V), 其中V 是该点的相邻点数量;
- 入度难算:对于有向图点的入度的计算难度较大,时间复杂度为 O(E),其中E是图中的边的数量;
邻接矩阵与邻接表对比
| 特性 | 邻接矩阵 | 邻接表 |
|---|---|---|
| 空间复杂度 | O(V²) (V为顶点数) | O(V + E)(E为边数) |
| 查询效率 | O(1)(直接访问matrix[i][j]) | O(k)(k为邻接表长度) |
| 适用场景 | 稠密图、频繁判断两顶点是否邻接 | 稀疏图、需要遍历邻接节点 |
| 加权扩展 | 矩阵存储权重值 | 使用Edge类存储目标顶点和权重 |
逆邻接表
逆邻接表从名字上就可以看出来和邻接表是逆的关系,这个逆就体现在入度和出度上。我们知道邻接表计算出度容易,计算入度难,而逆邻接表恰恰相反是计算入度容易,计算出度难。
如下图数组中存储点元素,而链表中存储的是以数组中的点为终点的起点元素。
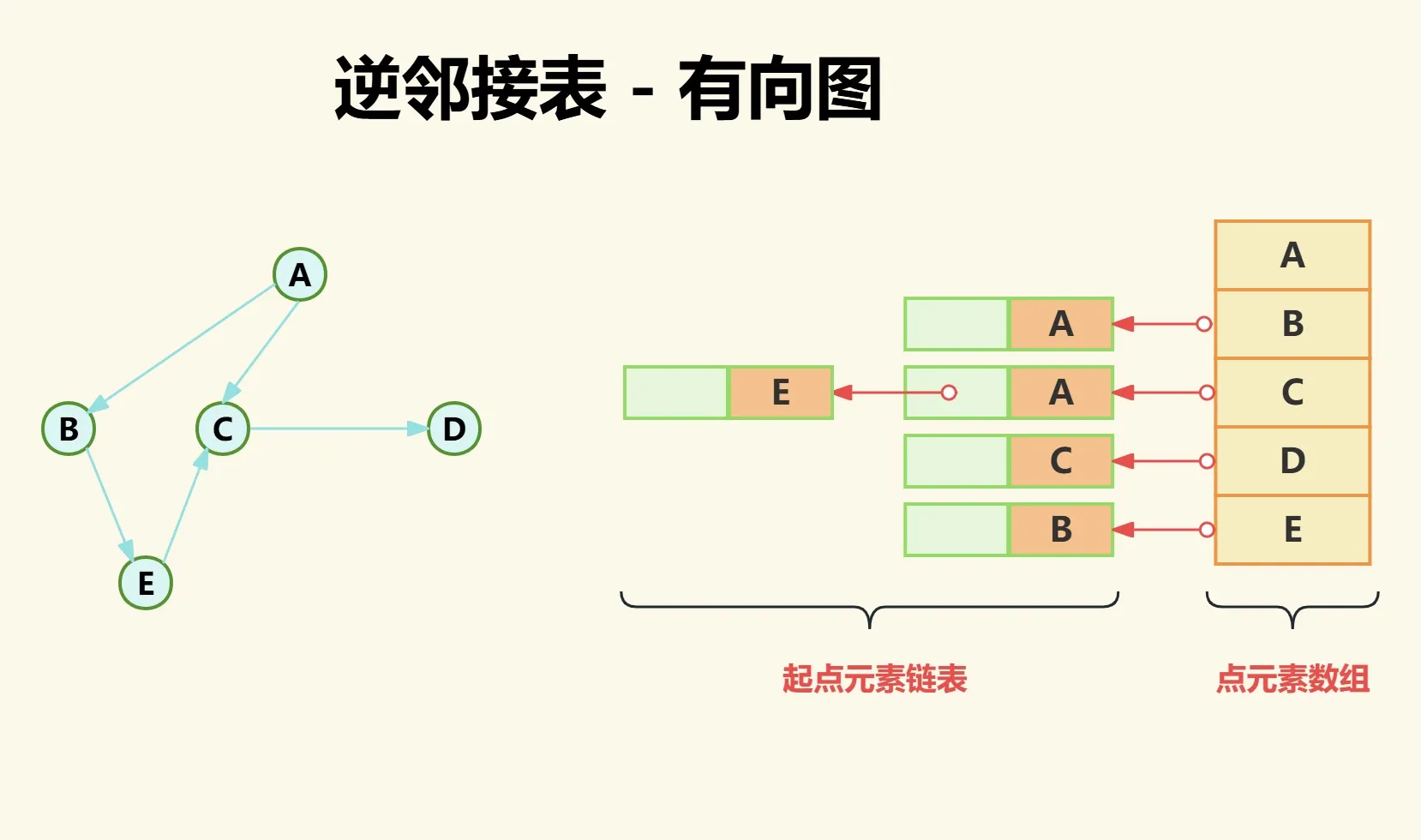
- 点A为终点的起点不存在;
- 点B为终点的起点为点A;
- 点D为终点的起点为点A和点E;
十字链表
邻接表出度计算容易,逆邻接表入度计算容易,那么有没有一种结构同时计算出度入度都容易呢?答案就是十字链表。
十字链表是邻接表和逆邻接表的结合体,每个点的边通过双向链表存储,同时记录了边的出度和入度。
下面我们详细讲解一下十字链表是怎么得到的。
(1)合并逆邻接表与邻接表
如下图我们之间把逆邻接表和邻接表拼接到一起,得到一个伪十字链表。
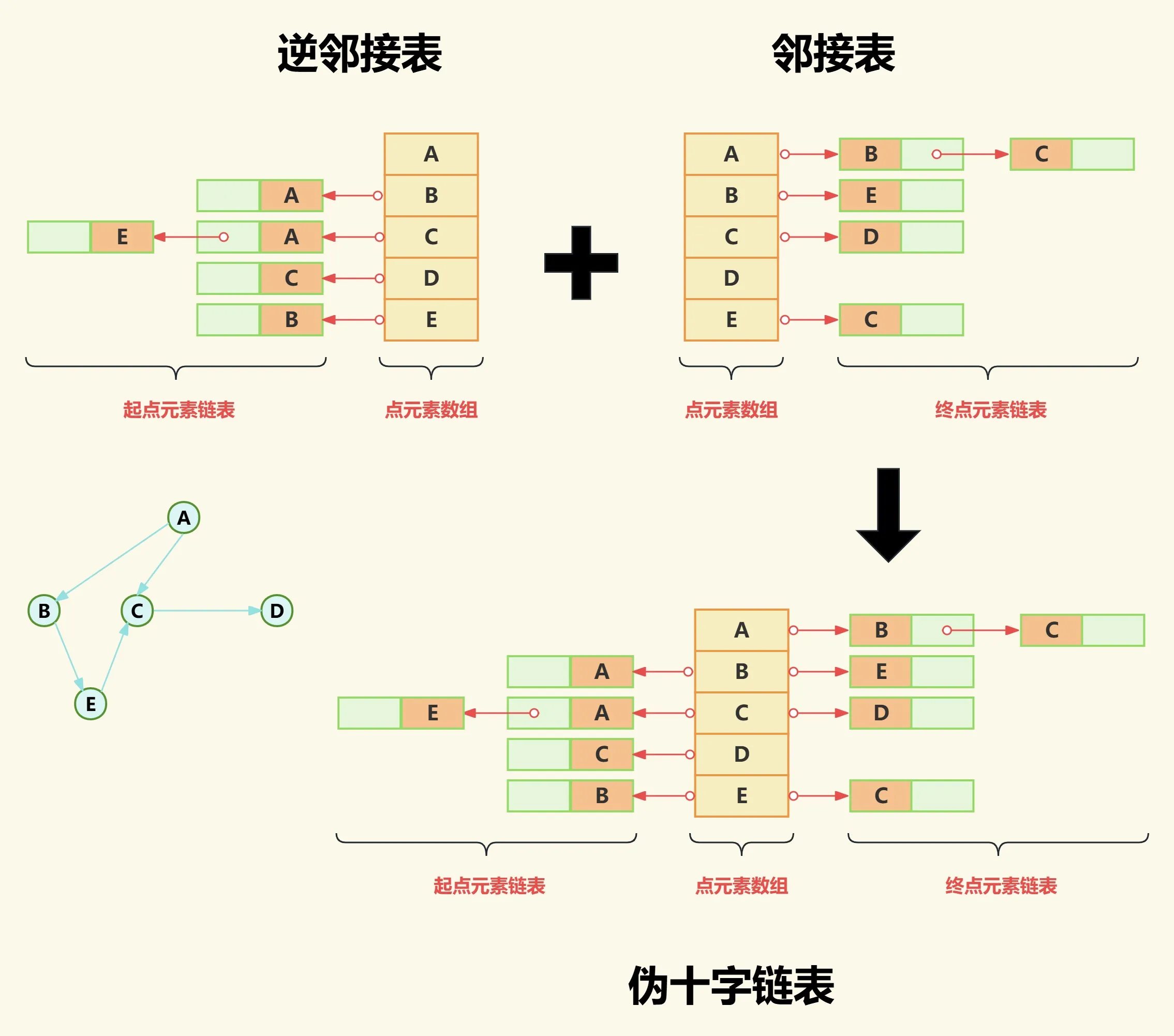
之所以称这个结合体为伪十字链表,是因为它虽然同时存储了边的两个方向,解决了出度入度计算问题,但是也引发了新的问题——存储效率低。
从上图不难看出链表中存在严重的重复存储的问题。要解决这个问题,我们先梳理一下我们得到的伪十字链表结构。
(2)链表由存点改存边
首先数组存储所有点,左侧链表存储起点元素集合,右侧链表存储终点元素集合;然后我们想为什么需要两条链表呢?因为一条链表就代表一个方向;
那第一步我们是否可以先解决方向的问题呢?而目前的结构节点只有一个点的信息,显然没有方向性,因此我们需要把链表节点改造成包含两个点的结构即起点和终点,这也意味着链表由原来存储点元素变为存储边元素。
原来点A出度链表存储点B和点C,现在改为存储[A->B]边和[A->C]边。
原来点B入度链表存储点A,现在改为存储[A->B]边。
如下图:
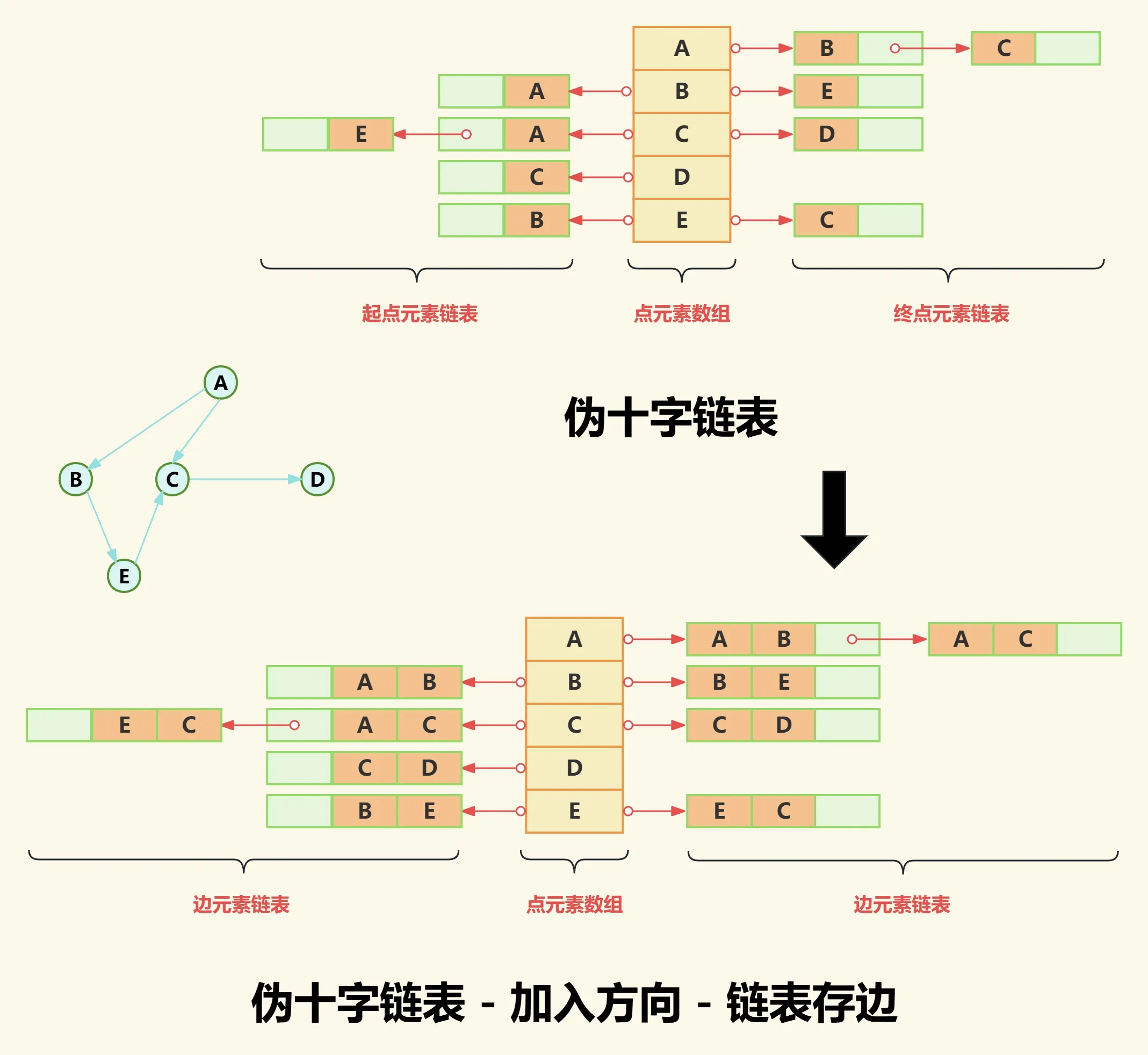
(3)删除重复元素
到这里就有条件解决重复的元素的问题了,比如上面链表中有两个[A->B]边,如果我们想把点B入度链表中[A->B]边删除,那么我们必须要有一个途径使得点B的入度链表可以和点A的出度链表中[A->B]边链接上。
首先数组元素结构应该至少包含:数据域|入边头节点指针|出边头节点指针;
然后链表节点元素结构应该至少包含:边起点下标|边终点下标|下一个入边节点指针域|下一个出边节点指针域;
下面我们进行去除重复元素,首先表里下出度链表结构,移除现有入度链表,其中入度链表中的元素指向到出度链表中,最后结果如下图:
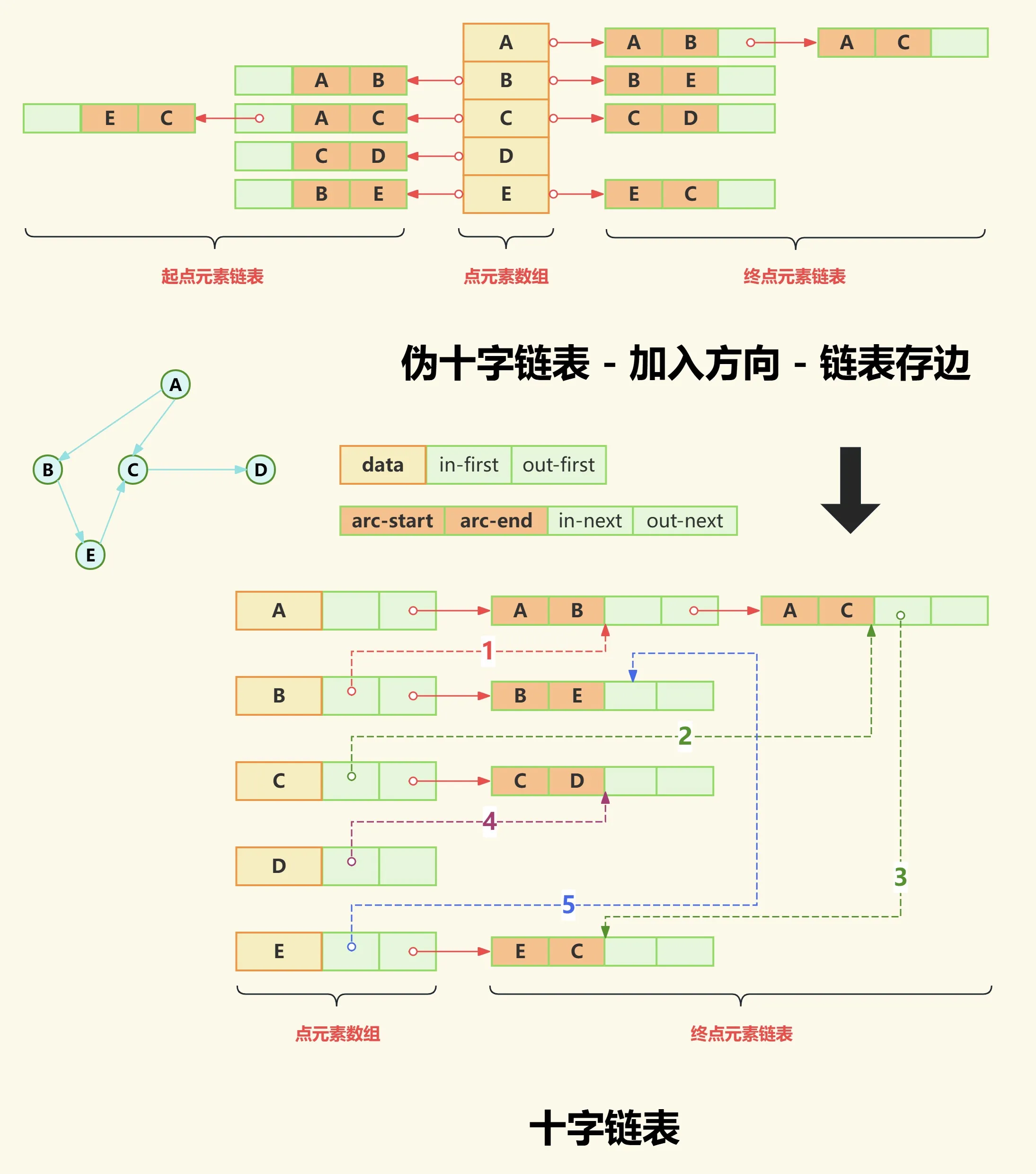
如上图红色实线箭头表示出度链表,而彩色虚线箭头表示入度链表。
- 点A为终点的边不存在,点A为起点的边为 [A->B]边和[A->C]边;
- 点B为终点的边为[A->B]边(即红色1号虚线),点B为起点的边为 [B->E]边;
- 点C为终点的边为[A->C]边(即绿色2号虚线)和[E->C]边(即绿色3号虚线),点C为起点的边为[C->D]边;
优缺点
优点:
- 高效存储,适合复杂的有向图,支持快速遍历;
- 快速计算出度入度;
缺点:
- 实现复杂,维护难度高;
图的遍历
图的遍历方式主要分为两种:广度优先遍历和深度优先遍历。
深度优先遍历(DFS)
深度优先遍历算法采用了回溯思想,从起始节点开始,沿着一条路径尽可能深入地访问节点,直到无法继续前进时为止,然后回溯到上一个未访问的节点,继续深入搜索,直到完成整个搜索过程。
因为遍历到的节点顺序符合「先进后出」的特点,所以深度优先搜索遍历可以通过「栈/递归」来实现。
特点:一路到底,逐层回退。
用途:解决找到所有解问题(找到起始–终点的所有路径,此时 DFS 空间占用少)。
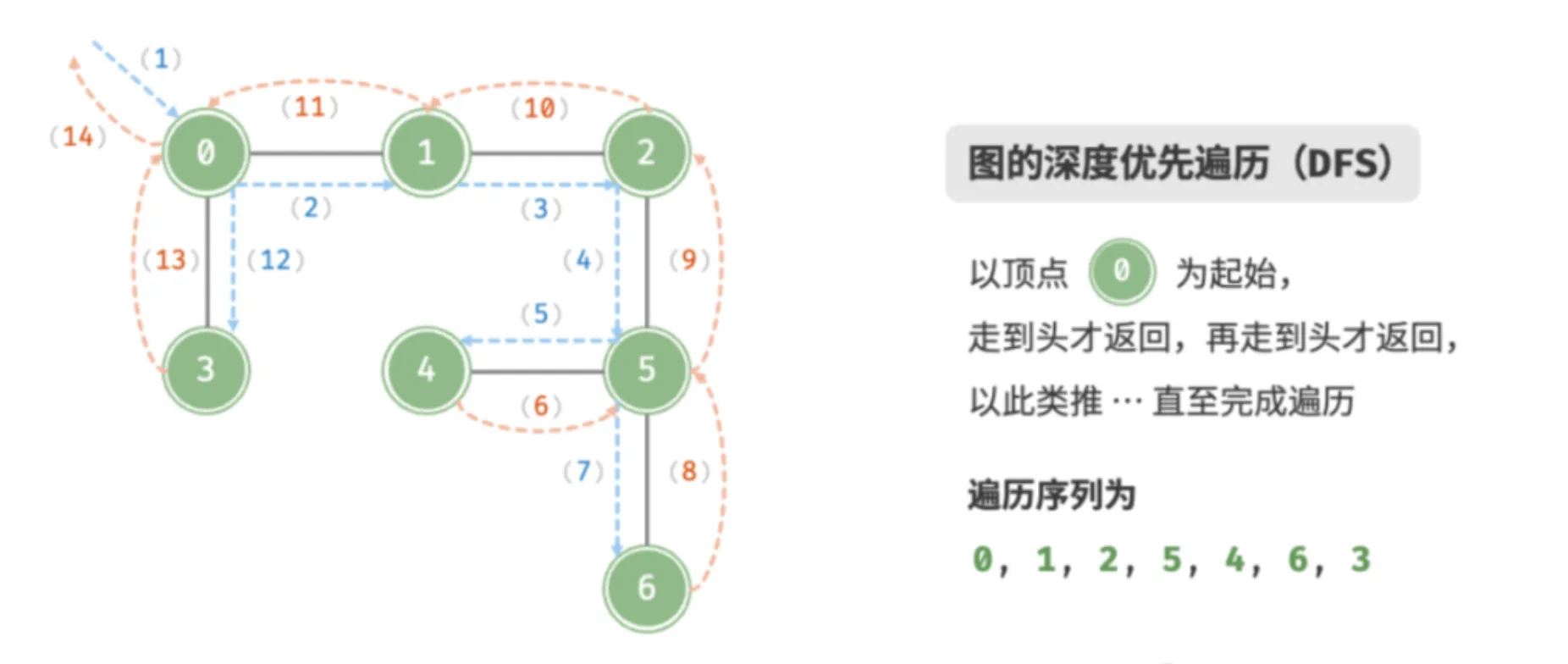
如上图所示:从左上角顶点出发,访问当前顶点的某个邻接顶点,直到走到尽头时返回,再继续走到尽头并返回,以此类推,直至所有顶点遍历完成。这种“走到尽头再返回”的算法范式通常基于栈/递归来实现。
- 直虚线代表向下递推,表示开启了一个新的递归方法来访问新顶点。
- 曲虚线代表向上回溯,表示此递归方法已经返回,回溯到了开启此方法的位置。
广度优先遍历(BFS)
广度优先遍历是一种由近及远的遍历方式,从某个节点出发,始终优先访问距离最近的顶点,并一层层向外扩张。以此类推,直到完成整个搜索过程。
因为遍历到的节点顺序符合「先进先出」的特点,所以广度优先遍历可以通过「队列」来实现。
特点:全面扩散,逐层递进。
用途:解决找到最优解的问题(找到的第一个起始–终点路径,即是最短路径)。
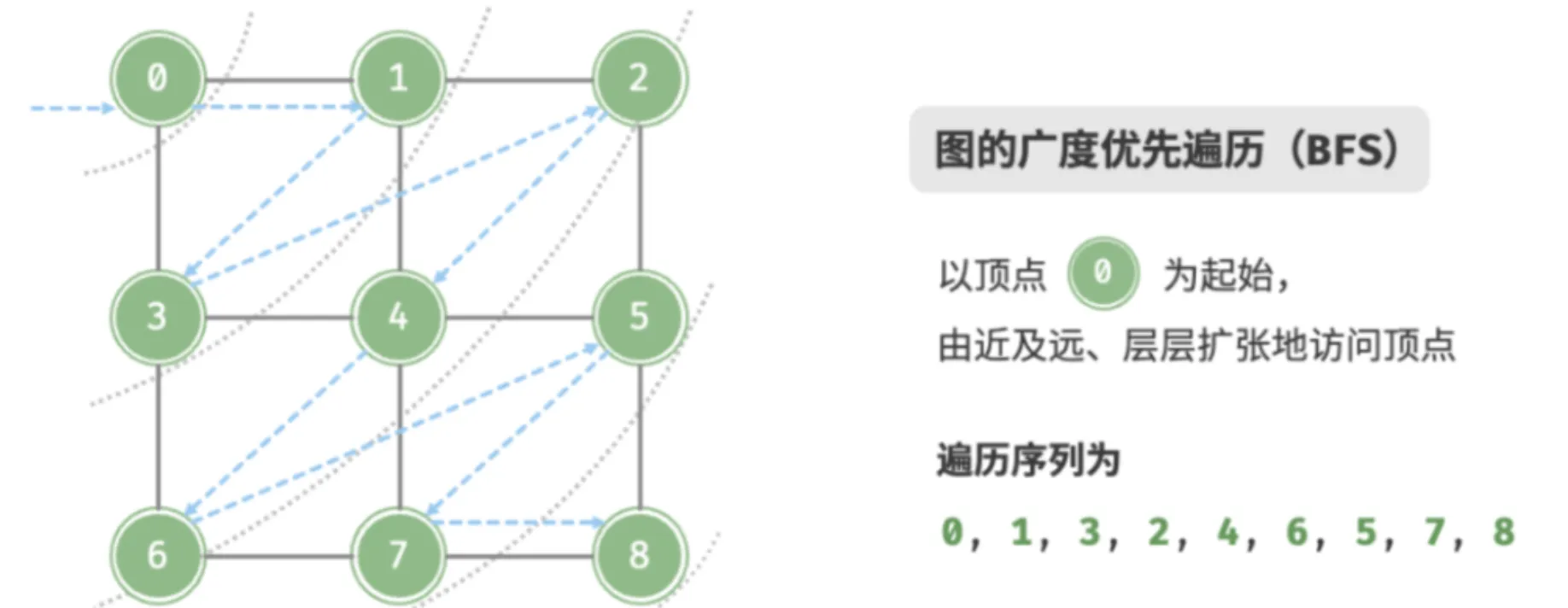
如上图所示:从左上角顶点出发,首先遍历该顶点的所有邻接顶点,然后遍历下一个顶点的所有邻接顶点,以此类推,直至所有顶点访问完毕。BFS 通常借助队列来实现,队列具有“先入先出”的性质,这与 BFS 的“由近及远”的思想 异曲同工。
代码实现
javaimport java.util.*;
public class Graph {
private int vertexCount; // 顶点总数
private List<List<Integer>> adj; // 邻接表
// 构造函数:初始化图
public Graph(int vertexCount) {
this.vertexCount = vertexCount;
adj = new ArrayList<>(vertexCount);
for (int i = 0; i < vertexCount; i++) {
adj.add(new LinkedList<>());
}
}
// 添加边(无向图)
public void addEdge(int v, int w) {
adj.get(v).add(w); // v→w
adj.get(w).add(v); // w→v(无向图需双向添加)
}
// 添加边(有向图)
public void addDirectedEdge(int v, int w) {
adj.get(v).add(w); // 仅v→w
}
// ------------------------- 广度优先遍历(BFS) -------------------------
public void bfs(int startVertex) {
boolean[] visited = new boolean[vertexCount]; // 访问标记数组
Queue<Integer> queue = new LinkedList<>(); // BFS队列
visited[startVertex] = true; // 标记起始顶点
queue.add(startVertex);
while (!queue.isEmpty()) {
int current = queue.poll();
System.out.print(current + " "); // 访问当前顶点
// 遍历所有邻接顶点
for (int neighbor : adj.get(current)) {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.add(neighbor);
}
}
}
}
// ------------------------- 深度优先遍历(DFS) -------------------------
public void dfs(int startVertex) {
boolean[] visited = new boolean[vertexCount];
dfsRecursive(startVertex, visited);
}
// DFS递归辅助方法
private void dfsRecursive(int current, boolean[] visited) {
visited[current] = true;
System.out.print(current + " "); // 访问当前顶点
for (int neighbor : adj.get(current)) {
if (!visited[neighbor]) {
dfsRecursive(neighbor, visited); // 递归访问未访问的邻接顶点
}
}
}
// ------------------------- 测试代码 -------------------------
public static void main(String[] args) {
// 创建无向图示例
Graph graph = new Graph(5);
graph.addEdge(0, 1); // 0-1
graph.addEdge(0, 4); // 0-4
graph.addEdge(1, 2); // 1-2
graph.addEdge(1, 3); // 1-3
graph.addEdge(2, 3); // 2-3
graph.addEdge(3, 4); // 3-4
System.out.println("广度优先遍历(从顶点0开始):");
graph.bfs(0); // 输出: 0 1 4 2 3
System.out.println("\n深度优先遍历(从顶点0开始):");
graph.dfs(0); // 输出: 0 1 2 3 4
}
}
代码解析
(1) 邻接表构建
- 无向图:调用 addEdge(v, w) 双向添加边(同时存储 v→w 和 w→v)。
- 有向图:调用 addDirectedEdge(v, w) 仅单向添加边。
(2) 广度优先遍历(BFS)
- 核心工具:队列(Queue)实现层次扩展。
- 时间复杂度:O(V+E)(V为顶点数,E为边数)。
- 应用场景:最短路径(无权图)、社交网络层级关系分析。
(3) 深度优先遍历(DFS)
- 核心工具:递归(或显式栈)实现深度探索。
- 时间复杂度:O(V+E)。
- 应用场景:拓扑排序、连通分量检测、迷宫求解。
总结
- BFS与DFS是图算法的基石,掌握其实现是理解复杂图算法(如最短路径、最小生成树)的关键。
- 邻接表适合大多数场景,尤其当图较稀疏时,空间效率显著优于邻接矩阵。
- 实际开发中可结合 JGraphT 等图库,快速实现高级功能。
图的经典算法
遍历算法:
深度搜索和广度搜索(必学)
最短路径算法:
Floyd,Dijkstra(必学)
最小生成树算法:
Prim,Kruskal(必学)
实际常用算法:
关键路径、拓扑排序(原理与应用)
二分图匹配:
配对、匈牙利算法(原理与应用)
拓展:
中心性算法、社区发现算法(原理与应用)
相关信息
图的算法后续单独列一篇文章
图的实际应用
- 社交网络分析:通过BFS实现好友推荐或六度分隔理论验证。
- 路径规划:地图导航中的最短路径计算(Dijkstra/A*算法)。
- 网络流量优化:最大流算法(如Dinic算法)解决资源分配问题。
- 推荐系统:基于图神经网络的用户-商品关系建模。


本文作者:柳始恭
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
