目录
学习了这么长时间的数据结构与算法,通过博客记录下个人的理解与总结,学习过程中多加思考,结合Java集合体系中的结构,思考换做自己要如何实现
数据结构
数据结构是算法的基石,只有掌握了数据结构,才能实现各种奇思妙想的算法
基本概念
数据结构整体分为线性结构、非线性结构的、散列表等,从物理存储的角度上来说,数据结构又分为物理结构和逻辑结构,物理结构只有数组、链表两种方式,逻辑结构基于数组、链表衍生出来的结构
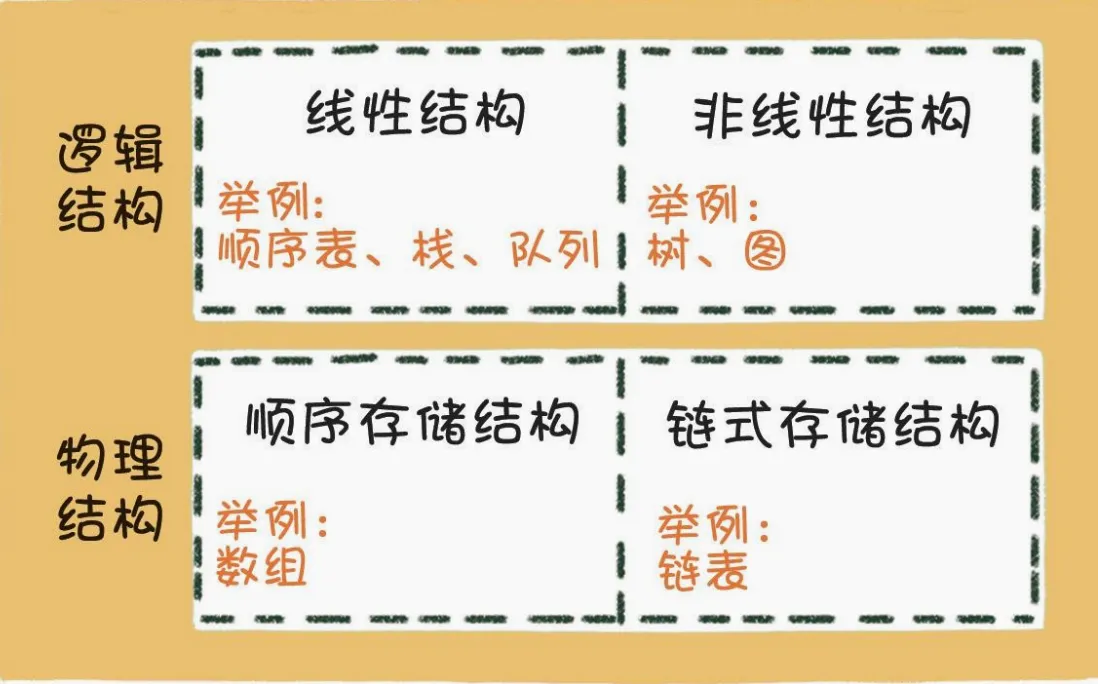
重点掌握
将上图牢记于心,在脑海中形成自己对数据结构概念理解的轮廓,所有的数据结构都可以基于物理结构(也就是数组、链表)进行实现,无非就是逻辑结构上贴合顺序存储方式或者是链式存储方式。
线性结构
线性结构是最简单的结构,其中的数据元素之间存在一种线性的关系,可以理解为是一种一维结构。 线性结构可以分为以下几种
数组
数组(array),是Java最基础常用的结构,数组中存储的称为元素。
特点:
- 数组创建以后,大小固定,是不可变的。
- 数组中的元素在内存中是连续存储的,天然有序。
- 每个元素对应着一个下标,可通过下标索引值快速定位到元素。
相关信息
在java中,最经典的莫过于ArrayList的实现,底层使用数组结构,查询、修改效率高,对于插入数据超过数组长度时进行动态扩容,删除中间元素时对元素进行迁移,有兴趣可以阅读下源码
链表
链表(Linked list)是一种链式结构,链表中的数据称为节点,每个节点数据中包含下一个节点的数据指针,一个链表由多个节点组成。
特点:
- 链表的长度可以动态改变,长度没有限制。
- 链表中的节点可以在内存中的任意位置,非连续存储。
- 通过指针来导航和访问链表中的元素。

根据以上特点,实现一个单向链表
javapublic class ListNode {
Object val;
ListNode next;
ListNode() {
}
ListNode(Object val) {
this.val = val;
}
ListNode(Object val, ListNode next) {
this.val = val;
this.next = next;
}
}
相关信息
链表的实现分为多种,以上只是单向链表的实现,还存在双向链表,还有单向/双向循环链表,本质就是节点中存在一个指向下一节点的引用与上一节点的引用,即为双向,循环链表的本质就是尾节点的下一个节点从指向null,变成指向头节点,而头节点的上一节点引用从null,变成了指向尾节点
数组与链表对比
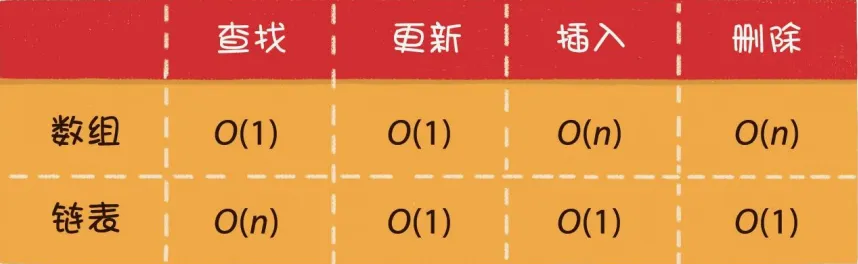
数组与链表本身既是物理结构,同时也是逻辑结构,他们的优势各不相同
数组适用于读多写少的场景
链表适用于频繁插入与删除的场景
在Java中,经常把集合ArrayList 与 LinkedList 进行对比,本质对比的就是底层上不同结构的实现
栈
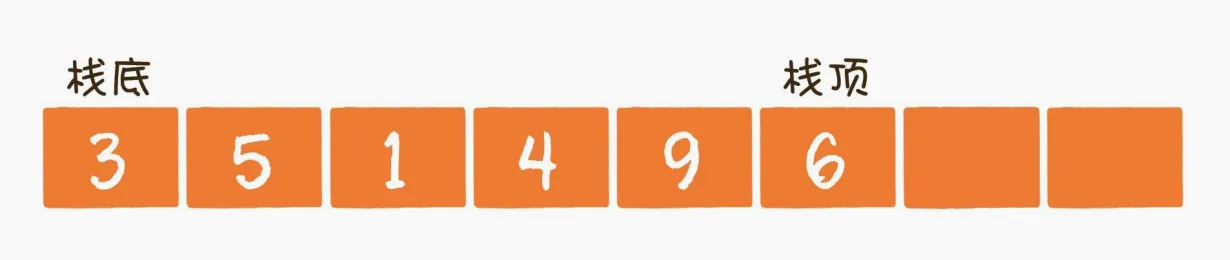
栈是一种特殊的线性数据结构,支持两种主要操作:压栈(push)和弹栈(pop),遵循先进后出(LIFO, Last In First Out)的原则。
实现方式:
数组:使用数组的一端作为栈顶,当需要压栈或出栈时,只需更新栈顶指针。
javapublic class ArrayStack<T> {
private static final int DEFAULT_CAPACITY = 10;
private Object[] elements;
private int top; // 栈顶指针
public ArrayStack() {
elements = new Object[DEFAULT_CAPACITY];
top = -1; // 初始化为空栈
}
// 入栈操作
public void push(T item) {
if (top == elements.length - 1) {
resize(); // 动态扩容
}
elements[++top] = item;
}
// 出栈操作
public T pop() {
if (isEmpty()) {
throw new EmptyStackException();
}
T item = (T) elements[top];
elements[top--] = null; // 帮助垃圾回收
return item;
}
// 查看栈顶元素
public T peek() {
if (isEmpty()) {
throw new EmptyStackException();
}
return (T) elements[top];
}
// 判断栈是否为空
public boolean isEmpty() {
return top == -1;
}
// 获取栈大小
public int size() {
return top + 1;
}
// 动态扩容方法
private void resize() {
int newSize = elements.length * 2;
Object[] newArray = new Object[newSize];
System.arraycopy(elements, 0, newArray, 0, elements.length);
elements = newArray;
}
}
链表:使用单向链表的头部作为栈顶,新元素总是添加到头部,出栈也是从头节点开始。

javapublic class LinkedListStack<T> {
// 链表节点定义
private static class Node<T> {
T data;
Node<T> next;
Node(T data) {
this.data = data;
this.next = null;
}
}
private Node<T> top; // 栈顶节点
private int size; // 栈大小
public LinkedListStack() {
top = null;
size = 0;
}
// 入栈操作
public void push(T item) {
Node<T> newNode = new Node<>(item);
newNode.next = top; // 新节点指向旧栈顶
top = newNode; // 更新栈顶指针
size++;
}
// 出栈操作
public T pop() {
if (isEmpty()) {
throw new EmptyStackException();
}
T item = top.data;
top = top.next; // 栈顶指针下移
size--;
return item;
}
// 查看栈顶元素
public T peek() {
if (isEmpty()) {
throw new EmptyStackException();
}
return top.data;
}
// 判断栈是否为空
public boolean isEmpty() {
return top == null;
}
// 获取栈大小
public int size() {
return size;
}
}
相关信息
栈结构更多的体现在历史的回溯上,在Java中,栈结构是我们接触的数据结构中最多的一种,我们常说的异常堆栈信息,就是使用栈,方法之间的调用都是通过栈来进行存储的。
队列
队列是一种只允许在一端进行插入操作,在另一端进行删除操作的线性数据结构,遵循先进先出(FIFO, First In First Out)的原则。
实现方式:
数组:使用数组实现 循环队列,通过调整指针来模拟循环,从而提高空间利用率。

javapublic class ArrayQueue<E> extends AbstractQueue<E> {
private static final int DEFAULT_CAPACITY = 10;
private Object[] elements;
private int head; // 队列头指针
private int tail; // 队列尾指针
private int size; // 当前元素数量
public ArrayQueue() {
elements = new Object[DEFAULT_CAPACITY];
head = 0;
tail = 0;
size = 0;
}
// 入队操作 (队列满时自动扩容)
@Override
public boolean offer(E e) {
if (size == elements.length) {
resize();
}
elements[tail] = e;
tail = (tail + 1) % elements.length;
size++;
return true;
}
// 出队操作
@Override
public E poll() {
if (size == 0) return null;
E element = (E) elements[head];
elements[head] = null; // 帮助垃圾回收
head = (head + 1) % elements.length;
size--;
return element;
}
// 查看队首元素
@Override
public E peek() {
return size == 0 ? null : (E) elements[head];
}
// 队列大小
@Override
public int size() {
return size;
}
// 动态扩容方法
private void resize() {
int newCapacity = elements.length * 2;
Object[] newArray = new Object[newCapacity];
// 将元素复制到新数组的连续位置
if (head < tail) {
System.arraycopy(elements, head, newArray, 0, size);
} else {
System.arraycopy(elements, head, newArray, 0, elements.length - head);
System.arraycopy(elements, 0, newArray, elements.length - head, tail);
}
elements = newArray;
head = 0;
tail = size;
}
// 迭代器实现(简化版)
@Override
public Iterator<E> iterator() {
return new Iterator<E>() {
private int cursor = 0;
@Override
public boolean hasNext() {
return cursor < size;
}
@Override
public E next() {
if (!hasNext()) throw new NoSuchElementException();
return (E) elements[(head + cursor++) % elements.length];
}
};
}
// 清空队列
@Override
public void clear() {
Arrays.fill(elements, null);
head = 0;
tail = 0;
size = 0;
}
}
链表:使用单向链表的头部和尾部作为队列的两端

javapublic class LinkedQueue<E> extends AbstractQueue<E> {
// 链表节点定义
private static class Node<E> {
E data;
Node<E> next;
Node(E data) {
this.data = data;
this.next = null;
}
}
private Node<E> head; // 队列头指针
private Node<E> tail; // 队列尾指针
private int size; // 队列大小
public LinkedQueue() {
head = null;
tail = null;
size = 0;
}
// 入队操作
@Override
public boolean offer(E e) {
Node<E> newNode = new Node<>(e);
if (tail == null) {
head = tail = newNode;
} else {
tail.next = newNode;
tail = newNode;
}
size++;
return true;
}
// 出队操作
@Override
public E poll() {
if (size == 0) return null;
E element = head.data;
head = head.next;
if (head == null) {
tail = null;
}
size--;
return element;
}
// 查看队首元素
@Override
public E peek() {
return size == 0 ? null : head.data;
}
// 队列大小
@Override
public int size() {
return size;
}
// 迭代器实现
@Override
public Iterator<E> iterator() {
return new Iterator<E>() {
private Node<E> current = head;
@Override
public boolean hasNext() {
return current != null;
}
@Override
public E next() {
if (!hasNext()) throw new NoSuchElementException();
E data = current.data;
current = current.next;
return data;
}
};
}
// 清空队列
@Override
public void clear() {
head = null;
tail = null;
size = 0;
}
}
相关信息
队列还有一些其他类型:优先队列、双端队列
优先队列:根据优先级进行出队,谁的优先级高谁先出队,其本质是在二叉堆的基础上进行实现。

双端队列:采用双向链表结构,可以从头部入队出队,也可以从尾部入队出队

哈希表
哈希表(hash table)也叫做散列表,这种数据结构提供了键(Key)与值(Value)的映射关系。只要给出一个Key,就可以高效查找到它所匹配的Value,时间复杂度接近于O(1).
实现原理
哈希表本质就是一个数组,Value就是数组中的数据,而Key一般是字符串,通过哈希函数算法将Key转换成数组的索引
哈希冲突
由于数组的长度是有限的,如果插入的Value值越来越多时,不同的Key通过哈希函数计算出来的索引下标可能会相同,这就是哈希冲突也叫做哈希碰撞
哈希冲突时无可避免的,解决的方式有很多种,最常用的是开放寻址法、链表法。
开放寻址法
开放寻址法的思路很简单,就是当Key通过哈希函数计算出来的索引下标位置存在数据时,就往后移一位看是否存在数据,直到找到为空的下标位置进行存储。
链表法
哈希表中的数组不仅是一个Enrty,还是链表的头节点。每个Enrty对象都通过next指针指向下一个Entry节点,当新来的Entry的索引下标存在数据冲突时,则将当前Entry插入到链表的尾部即可。
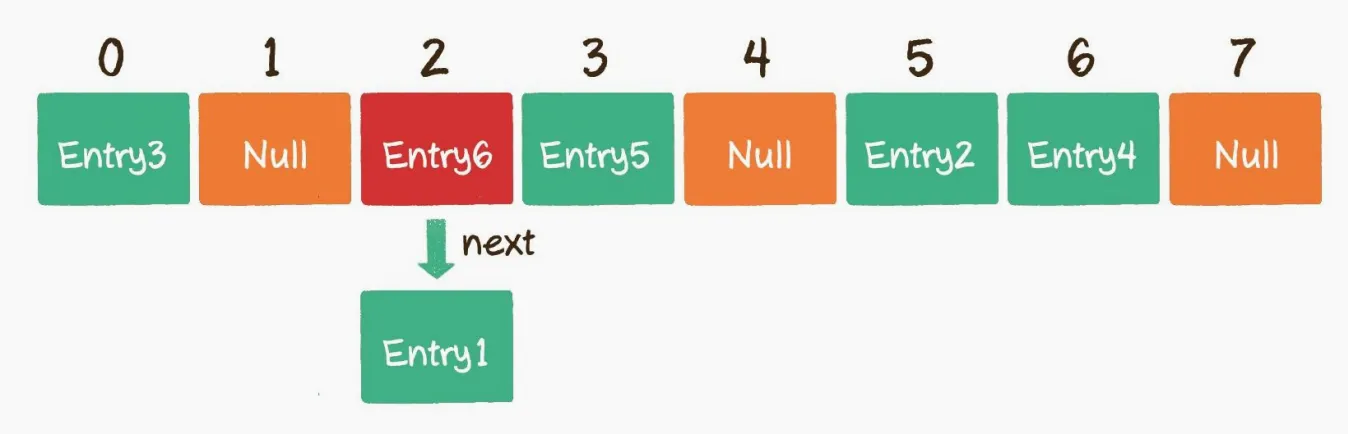
当读取数据的时,根据当前哈希函数计算的索引位置,找到链表的头节点,然后从链表中找到Key对应的Enrty。
思考?当链表过长时,读取效率下降如何处理
在极端情况下,如果很多键都映射到同一个桶(bucket),链表会变得很长,导致查询效率从O(1)退化为O(n),性能下降明显。
回想下 HashMap 的源码实现,看下 HashMap 在 JDK1.8 中是如何优化链表过长问题的。
HashMap 的优化:
到了Java 8,HashMap 引入了红黑树来优化这个问题。当链表的长度超过一定阈值时,链表会被转换成红黑树,这样查询的时间复杂度可以维持在O(log n),比链表的O(n)要好很多。
当链表长度超过默认阈值8,且数组长度大于等于64时,才会将链表转换为红黑树。如果数组长度小于64,即使链表长度超过8,HashMap会选择先进行数组扩容,而不是立即转换结构。这是因为扩容可以减少哈希碰撞的概率,可能比转换为树更有效。
另外,红黑树的结构相比链表,虽然查询效率高,但插入和删除操作更复杂,需要维护树的平衡,所以在节点较少时,链表的性能可能更好。因此,HashMap在节点减少到6时会转换回链表,这样可以避免在频繁插入和删除时反复转换带来的性能损耗。
总结一下,HashMap解决链表过长的问题主要通过两个方法:一是当链表长度超过阈值且数组容量足够大时,将链表转为红黑树;二是通过扩容数组来减少哈希碰撞,从而间接减少链表长度。这两种方法结合起来,保证了HashMap在大多数情况下的高效性能。


本文作者:柳始恭
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
