大家可能会想，怎么评估一个算法的好坏呢？ 本章节就是在学习算法前，先需要掌握一些理论基础。

评估算法优劣的核心指标是什么？

时间复杂度 O(f(n))

把某个算法执行步骤的计数来作为衡量运行时间的标准

衡量标准

在一个完全理想状态下的计算机中，我们定义 T(n)来表示程序执行所要花费的时间，其中n代表数据输入量。当然程序的最坏运行时间(Worse Case Executing Time)或最大运行时间是时间复杂度衡量的标准。

时间复杂度的衡量标准，一般以 Big-Oh 表示。常见的 Big-Oh

Big-Oh	名称	描述
O(1)	常数时间(Constant Time)	表示算法的运行时间是一个常数倍
O(n)	称为线性时间(Linear Time)	表示执行的时间会随着数据集合的大小而线性增长
O(log2n)	次线性时间(Sub-Linear Time)	成长速度比线性时间慢，而比常数时间快
O(n^2)	平方时间(Quadratic Time)	称为，算法的运行时间会成二次方的增长
O(n^3)	立方时间(Cubic Time)	算法的运行时间会成三次方的增长
O(2^n)	指数时间(Exponential Time)	算法的运行时间会成2 的 n 次方增长。例如，解决Nonpolynomial Problem 问题算法的时间复杂度为 O(2")
O(nlog2n)	线性乘对数时间	称为，介于线性和二次方增长的中间模式

由于在估算算法复杂度时采取“宁可高估不要低估”的原则，因此估计出来的复杂度是算法真正所需运行时间的上限。请大家看以下范例，以了解时间复杂度的意义。

范例：假如运行时间 T(n)=3㎡'+2㎡+5n，求时间复杂度。

解答：首先找出常数c与 n。当 n=0、c=10 时，若 n>no，则 3n'+2㎡'+5n<10㎡，因此得知时间复杂度为 O(m^3)。

时间复杂度的意义

上面的范例中抹掉了好多东西，只剩下了一个最高阶项啊… 那这个东西有什么意义呢？

时间复杂度的意义在于

当我们要处理的样本量很大很大时，我们会发现低阶项是什么不是最重要的；每一项的系数是什么，不是最重要的。真正重要的就是最高阶项是什么。

这就是时间复杂度的意义，它是衡量算法流程的复杂程度的一种指标，该指标只与数据量有关，与过程之外的优化无关。

成长率

在分析算法的时间复杂度时，往往用函数来表示它的成长率(Rate ofGrowth)，其实时间复杂度是一种“渐近表示法”(Asymptotic Notation)

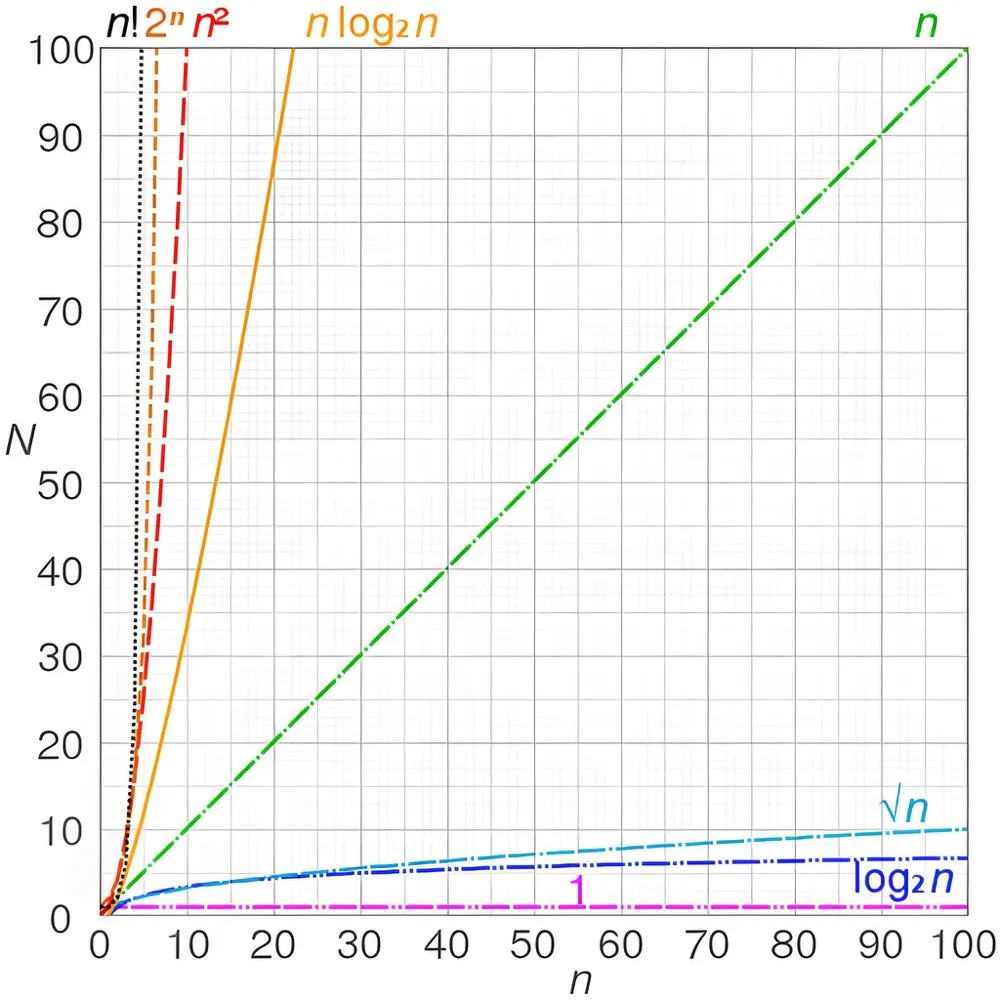
不同的时间复杂度之间在不同数量下的处理速率

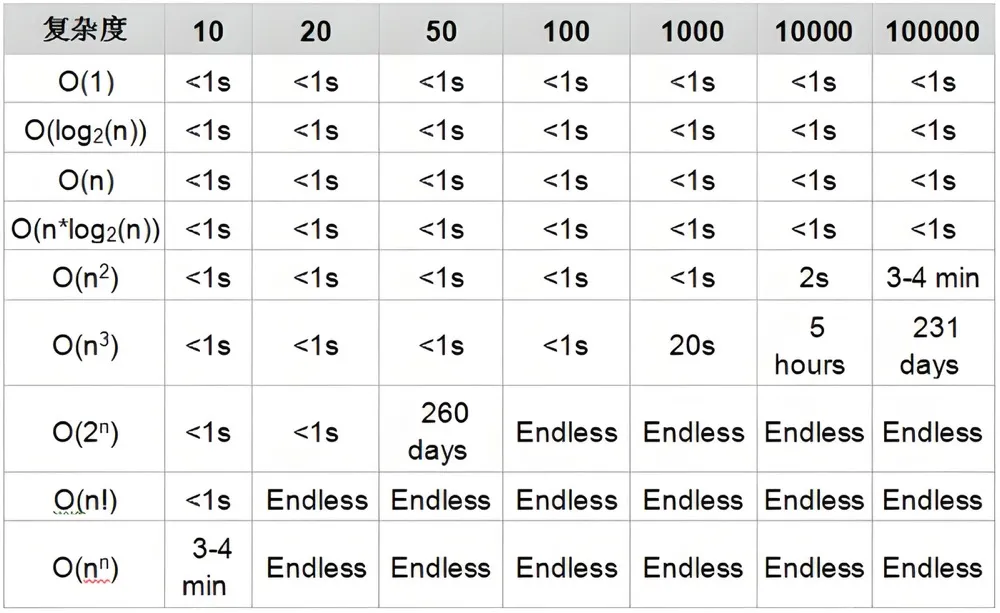
空间复杂度

你要实现一个算法流程，在实现算法流程的过程中，你需要开辟一些空间来支持你的算法流程。

• 作为输入参数的空间，不算额外空间。
• 作为输出结果的空间，也不算额外空间。

因为这些都是必要的、和现实目标有关的。所以都不算。

但除此之外，你的流程如果还需要开辟空间才能让你的流程继续下去。这部分空间就是额外空间，如果你的流程只需要开辟有限几个变量，额外空间复杂度就是O(1)。

常见的空间复杂度有下面几种情形。

常量空间

当算法的存储空间大小固定，和输入规模没有直接的关系时，空间复杂度记作O(1)。例如 int i=3

线性空间

当算法分配的空间是一个线性的集合(如列表)，并且集合大小和输入规模n成正比时，空间复杂度记作O(n)。例如 int[] array = {1,2,3}

二维空间

当算法分配的空间是一个二维列表集合，并且集合的长度和宽度都与输入规模n成正比时，空间复杂度记作O(n2)。例如 int[][] array = new int[10][10]

递归空间

递归是一个比较特殊的场景。虽然递归代码中并没有显式地声明变量或集合，但是计算机在执行程序时，会专门分配一块内存，用来存储“函数调用栈”。

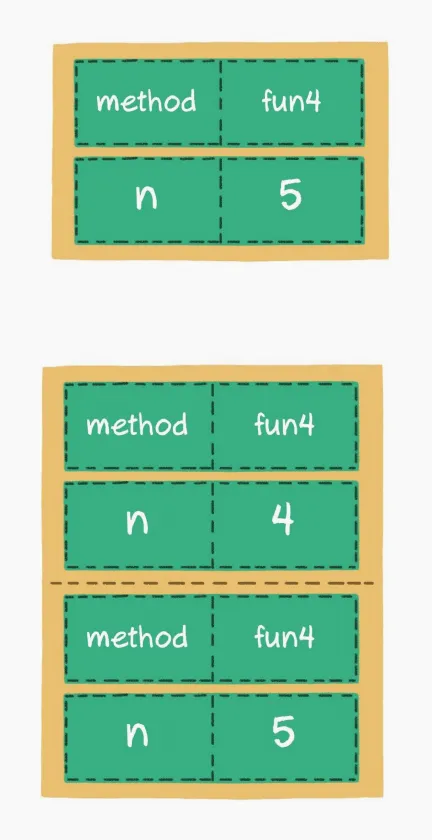
由上面“函数调用栈”的出入栈过程可以看出，执行递归操作所需要的内存空间和递归的深度成正比。纯粹的递归操作的空间复杂度也是线性的，如果递归的深度是n，那么空间复杂度就是O(n)。

时间与空间的取舍

人们之所以花大力气去评估算法的时间复杂度和空间复杂度，其根本原因是计算机的运算速度和空间资源是有限的。虽然目前计算机的CPU处理速度不断飙升，内存和硬盘空间也越来越大，但是面对庞大而复杂的数据和业务，我们仍然要精打细算，选择最有效的使用方式。

但是，正所谓鱼和能掌不可兼得。很多时候，我们不得不在时间复杂度和空间复杂度之间进行取舍。

java
public class DuplicateExample {
    // 方案 1：暴力法（时间换空间）
    // 时间复杂度 O(n²)，空间复杂度 O(1)
    public static boolean hasDuplicateBruteForce(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[i] == nums[j]) {
                    return true;
                }
            }
        }
        return false;
    }

    // 方案 2：哈希表（空间换时间）
    // 时间复杂度 O(n)，空间复杂度 O(n)
    public static boolean hasDuplicateHashSet(int[] nums) {
        Set<Integer> seen = new HashSet<>();
        for (int num : nums) {
            if (seen.contains(num)) {
                return true;
            }
            seen.add(num);
        }
        return false;
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 1};
        
        // 暴力法：通过双重循环比较所有元素对，省去额外空间，但时间效率低。
        System.out.println("暴力法结果: " + hasDuplicateBruteForce(nums)); // true
        
        // 哈希表：用 HashSet 存储已遍历元素，以空间换时间，效率更高。
        System.out.println("哈希表结果: " + hasDuplicateHashSet(nums));    // true
    }
}

在绝大多数时候，时间复杂度更为重要一些，我们宁可多分配一些内存空间，也要提升程序的执行速度。

取舍策略总结

1. 时间换空间：当内存资源紧张时（如嵌入式系统），选择低空间复杂度的算法。
2. 空间换时间：当时间要求严格时（如高频交易系统），选择低时间复杂度的算法。
3. 平衡选择：根据实际场景的数据规模（如 n 的大小）和硬件条件灵活调整。

常数项时间（实现细节决定）

如果一个操作的执行时间不以具体样本量为转移，每次执行时间都是固定时间，称这样的操作为常数时间的操作。

常见的常数时间的操作

• 算术运算（+、-、*、/、% 等）
• 位运算（>>、>>>、<<、|、&、^等）
• 赋值、比较、自增、自减操作等
• 数组寻址操作

总之，执行时间固定的操作都是常数时间的操作。反之，执行时间不固定的操作，都不是常数时间的操作。

算法流程的常数项

我们会发现，时间复杂度这个指标，是忽略低阶项和所有常数系数的，难道同样时间复杂度的流程，在实际运行时候就一样的好吗？

结果当然不是，时间复杂度只是一个很重要的指标而已，如果两个时间复杂度一样的算法，你还要去在时间上拼优劣，就进入到拼常数时间的阶段，简称拼常数项。

算法流程的常数项的比拼方式

放弃理论分析，生成随机数据直接测。

为什么不去理论分析？

不是不能纯分析，而是没必要。因为不同常数时间的操作，虽然都是固定时间，但还是有快慢之分的。 比如，位运算的常数时间原小于算术运算的常数时间，这两个运算的常数时间又远小于数组寻址的时间。所以如果纯理论分析，往往会需要非常多的分析过程。都已经到了具体细节的程度，莫不如交给实验数据好了。

如何确定算法流程的总操作数量与样本数量之间的表达式关系？

1. 想象该算法流程所处理的数据状况，要按照最差情况来。
2. 把整个流程彻底拆分为一个个基本动作，保证每个动作都是常数时间的操作。
3. 如果数据量为N，看看基本动作的数量和N是什么关系。

位运算

位运算直接操作整数的二进制位，是计算机底层最高效的操作方式之一。Java中支持的位运算符包括：

运算符	名称	描述	示例（二进制）
&	按位与	两数对应位均为1时结果为1	1010 & 1100 = 1000
|	按位或	两数对应位任一为1时结果为1	1010
^	按位异或	两数对应位不同时结果为1	1010 ^ 1100 = 0110
~	按位取反	单目运算符，所有位取反	~1010 = 0101（补码）
<<	左移	左移指定位数，低位补0	1010 << 2 = 101000
>>	算术右移	右移指定位数，高位补符号位	1010 >> 2 = 1110
>>>	逻辑右移	右移指定位数，高位补0	1010 >>> 2 = 0010

示例代码

位运算的用法

java
// 位运算符
int c = 0b1010; // 10（二进制）
int d = 0b0110; // 6（二进制）
System.out.println("\n----- 位运算符 -----");
System.out.println("c & d : " + (c & d));  // AND → 0010 → 2
System.out.println("c | d : " + (c | d));  // OR → 1110 → 14
System.out.println("c ^ d : " + (c ^ d));  // XOR → 1100 → 12
System.out.println("~c : " + (~c));       // 补码 → -11（十进制）
System.out.println("c << 2 : " + (c << 2)); // 左移2位 → 40
System.out.println("c >> 1 : " + (c >> 1)); // 右移1位 → 5
System.out.println("c >>> 1 : " + (c >>> 1)); // 无符号右移 → 5
print(1);
print(0);
print(-1);

// 输出二进制
static void print(int num){
    for (int i = 31; i >= 0; i--) {
        System.out.print((num & (1 << i)) == 0 ? "0" : "1");
    }
    System.out.println();
}

权限控制（位掩码）

java
public class PermissionSystem {
    // 权限标志位定义
    public static final int READ = 1 << 0;    // 0001
    public static final int WRITE = 1 << 1;   // 0010
    public static final int EXECUTE = 1 << 2; // 0100

    private int permissions = 0; // 初始无权限

    // 添加权限
    public void addPermission(int perm) {
        permissions |= perm;
    }

    // 移除权限
    public void removePermission(int perm) {
        permissions &= ~perm;
    }

    // 检查权限
    public boolean hasPermission(int perm) {
        return (permissions & perm) != 0;
    }

    public static void main(String[] args) {
        PermissionSystem user = new PermissionSystem();
        user.addPermission(READ | WRITE);
        System.out.println(user.hasPermission(READ));  // true
        System.out.println(user.hasPermission(EXECUTE)); // false
    }
}

交换变量值

java
int a = 5, b = 3;
a = a ^ b; // a = 5 ^ 3 = 6
b = a ^ b; // b = 6 ^ 3 = 5
a = a ^ b; // a = 6 ^ 5 = 3
System.out.println(a + ", " + b); // 3, 5

位运算实际应用场景

1. 性能优化

• 用位运算替代乘除法：x << 1 等价于 x * 2
• 快速判断奇偶性：(x & 1) == 0

2. 数据压缩

• 将多个布尔值压缩到一个整型变量中（如权限系统）

3. 加密算法

• 异或加密：data ^ key

4. 位图算法（BitMap）

• 海量数据去重与排序（如处理10亿个不重复整数）

面试、比赛、刷题中，一个问题的最优解是什么意思？

一般情况下，认为解决一个问题的算法流程，在时间复杂度的指标上，一定要尽可能的低，先满足了时间复杂度最低这个指标之后，使用最少的空间的算法流程，叫这个问题的最优解。

一般说起最优解都是忽略掉常数项这个因素的，因为这个因素只决定了实现层次的优化和考虑，而和怎么解决整个问题的思想无关。

复杂度的估算

1. 算法的过程，和具体的语言是无关的。
2. 想分析一个算法流程的时间复杂度的前提，是对该流程非常熟悉
3. 一定要确保在拆分算法流程时，拆分出来的所有行为都是常数时间的操作。这意味着你写算法时，对自己的用过的每一个系统api，都非常的熟悉。否则会影响你对时间复杂度的估算。